Hướng dẫn cách khảo sát và vẽ đồ thị hàm số bậc ba chi tiết

Hướng dẫn cách khảo sát và vẽ đồ thị hàm số bậc ba chi tiết

Cách khảo sát và vẽ các dạng đồ thị hàm số trong đó có cách khảo sát và vẽ đồ thị hàm số bậc ba là phần kiến thức trọng tâm của chương trình Toán 10,11 và 12 có nhiều trong các đề thi quan trọng. Để giúp các em nắm rõ hơn phần kiến thức quan trọng này, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Bạn theo dõi nhé !

I. HÀM SỐ BẬC BA LÀ GÌ ?

This post: Hướng dẫn cách khảo sát và vẽ đồ thị hàm số bậc ba chi tiết

Trong đại số, một hàm số bậc ba là một hàm số có dạng:

f(x)=ax³+bx²+cx+d (trong đó a#0)

Phương trình f(x) = 0 là một phương trình bậc ba có dạng: ax³+bx²+cx+d =0
Các giá trị x thỏa mãn phương trình này được gọi là các nghiệm số của đa thức f(x).

II. CÁCH KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ BẬC BA

1. Cách khảo sát sự biến thiên của đồ thị hàm số bậc ba

Để khảo sát đồ thị hàm số bậc ba y=ax3+bx2+cx+d với a#0 ta thực hiện các bước sau:

+ Bước 1. Tập xác định: D=R.
+ Bước 2. Đạo hàm: y′=3ax2+2bx+c, Δ′=b2–3ac.
Δ′>0: Hàm số có 2 cực trị.
Δ′≤0: Hàm số luôn tăng hoặc luôn giảm trên R.
+ Bước 3. Đạo hàm cấp 2: y”=6ax+2b, y”=0⇔x=–b3a.
x=–b3a là hoành độ điểm uốn, đồ thị nhận điểm uốn làm tâm đối xứng.
+ Bước 4. Giới hạn:
Nếu a>0 thì: limx→–∞⁡y=–∞, limx→+∞⁡y=+∞.
Nếu a<0 thì: limx→–∞⁡y=+∞, limx→+∞⁡y=–∞.
+ Bước 5. Bảng biến thiên và đồ thị:
Trường hợp a>0:
+ Δ′=b2–3ac>0: Hàm số có 2 cực trị.

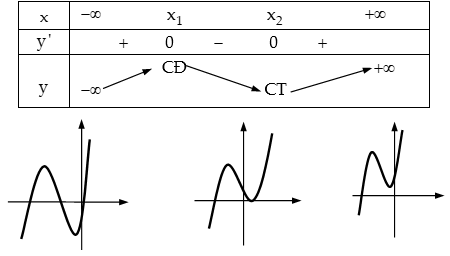
+ Δ′=b2–3ac≤0 ⇒y′≥0,∀x∈R: Hàm số luôn tăng trên R.

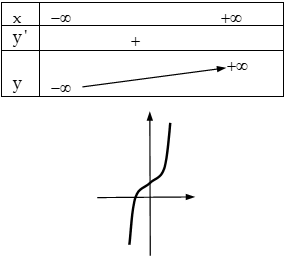
Trường hợp a<0:
+ Δ′=b2–3ac>0: Hàm số có 2 cực trị.

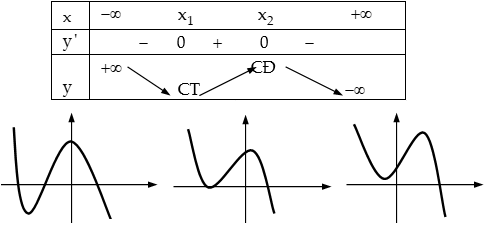
+ Δ′=b2–3ac≤0 ⇒y′≤0,∀x∈R: Hàm số luôn giảm trên R.

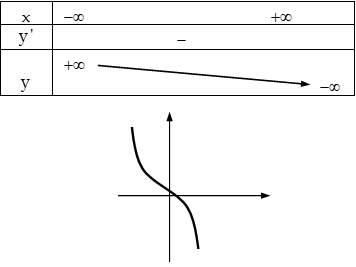
2. Các bước vẽ đồ thị hàm số bậc ba

Để vẽ đồ thị hàm số bậc 3 các bạn thực hiện theo các bước sau:

• Bước 1: Tìm tọa độ giao điểm của đồ thị với các trục tọa độ
• Bước 2: Xác định điểm đối xứng (nếu có)
• Bước 3: Xác định tính tuần hoàn của hàm số (nếu có)
• Bước 4: Dựa vào bảng biến thiên đã lập và những yếu tố xác định ở trên để vẽ đồ thị hàm số. Hình dạng của đồ thị hàm số sẽ dựa vào bảng biến thiên.

3. Ví dụ: Khảo sát sự biến thiên và vẽ đồ thị của hàm số : y = x³ + 3x² – 4 

a. Tập xác định D = R

b. Sự biến thiên

+)Giới hạn hàm số tại vô cực

; 

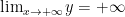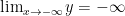
+)Chiều biến thiên:

y’ = 3x² + 6x

Cho y’ = 0 <=>  3x² + 6x = 0 <=> [x=0x=−2[x=0x=−2

 Hàm số đồng biến trong khoảng (-∞; -2) và (0; +∞)

Hàm số nghịch biến trong khoảng (-2; 0)

+) Cực trị

Hàm số đạt cực đại tại x = -2; yCD=y(−2)=0yCD=y(−2)=0

Hàm số đạt cực tiểu tại x = 0; yCT=y(0)=−4yCT=y(0)=−4

+)Lập bảng biến thiên :

x	-∞	-2	0	+∞
y’	+	0         –	0         +
y	-∞	0	-4	+∞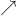

c. Đồ thị

Giao của đồ thị với trục Ox: y = 0 <=> x³ + 3x² – 4 = 0 <=> (x−1)(x+2)2=0(x−1)(x+2)2=0

<=> [x=1x=−2[x=1x=−2

Vậy (-2;0) và (1;0) là các giao điểm của đồ thị với trục Ox

Giao điểm của đồ thị với trục Oy: x = 0 <=> y = -4. Vậy (0;-4) là giao điểm của đồ thị với trục Oy. 

Bảng giá trị :

x	-2	-1	0	1
y	0	-2	-4	0

 Tìm điểm uốn

 y’’= 6x + 6

Cho y’’ = 0 <=>  6x + 6 = 0 <=> x = -1 => y = -2

Đồ thị hàm số có điểm uốn : U(-1, -2)

Vẽ đồ thị (C) :

Kết luận: Đồ thị hàm số bậc 3 đã cho nhận điểm U(-1;-2) làm tâm đối xứng.

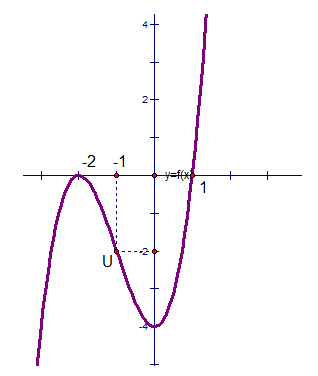
4. Các dạng đồ thị hàm số bậc ba: y = ax³ + bx² + cx + d (a ¹ 0)

III. BÀI TẬP KHẢO SÁT VÀ VẼ ĐỒ THỊ HÀM SỐ BẬC BA

Bài 1. Cho hàm số y=–x3+3×2+1 có đồ thị (C).
a. Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số.
b. Viết phương trình tiếp tuyến của đồ thị (C) tại A(3;1).

GIẢI:

a. Khảo sát sự biến thiên và vẽ đồ thị:
Tập xác định: D=R.
Chiều biến thiên:
Ta có: y′=–3×2+6x=–3x(x–2).
y′=0⇔–3x(x–2)=0 ⇔x=0 hoặc x=2.
y′>0⇔x∈(0;2), y′<0 ⇔x∈(–∞;0)∪(2;+∞).
Hàm số nghịch biến trên mỗi khoảng (–∞;0) và (2;+∞), đồng biến trên khoảng (0;2).
Hàm số đạt cực đại tại điểm x=2, giá trị cực đại của hàm số là y(2)=5.
Hàm số đạt cực tiểu tại điểm x=0, giá trị cực tiểu của hàm số là y(0)=1.
Giới hạn của hàm số tại vô cực: limx→–∞⁡y=+∞, limx→+∞⁡y=–∞.
Bảng biến thiên:

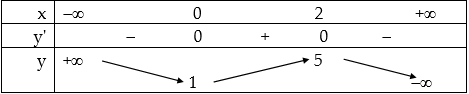
Đồ thị:

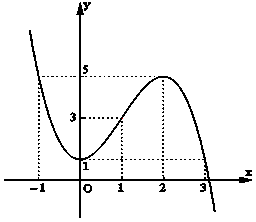
b. Phương trình tiếp tuyến của (C) tại điểm A(3;1) có dạng:
y–1=y′(3).(x–3) ⇔y=–9(x–3)+1 ⇔y=–9x+28.

Bài 2:. Cho hàm số y=2×3–9×2+12x–4 có đồ thị (C).
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số.
b. Tìm m để phương trình sau có 6 nghiệm phân biệt: 2|x|3–9×2+12|x|=m.

GIẢI:

a. Bảng biến thiên:

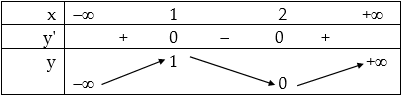
Đồ thị:

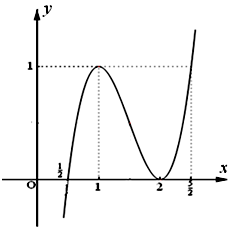
b. Ta có:
2|x|3–9×2+12|x|=m ⇔2|x|3–9×2+12|x|–4 =m–4.
Gọi (C):y=2×3–9×2+12x–4 và (C′):y=2|x|3–9×2+12|x|–4.
Ta thấy khi x≥0 thì: (C′):y=2×3–9×2+12x–4.
Mặt khác hàm số của đồ thị (C′) là hàm số chẵn nên (C′) nhận Oy là trục đối xứng. Từ đồ thị (C) ta suy ra đồ thị (C′) như sau:
+ Giữ nguyên phần đồ thị (C) bên phải trục Oy, ta được (C′1).
+ Lấy đối xứng qua trục Oy phần (C′1), ta được (C′2).
+ (C′)=(C′1)∪(C′2).

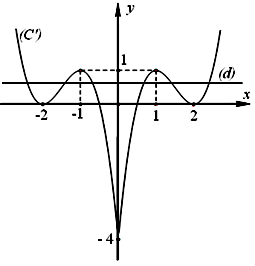
Số nghiệm của phương trình: 2|x|3–9×2+12|x|=m ⇔2|x|3–9×2+12|x|–4=m–4 là số giao điểm của đồ thị (C′) và đường thẳng (d):y=m–4.
Từ đồ thị (C′), ta thấy yêu cầu bài toán: ⇔0<m–4<1 Suy ra 4<m<5

Bài 3: Khảo sát sự biến thiên và vẽ đồ thị (C) của hàm số:
a. y=–x3+3×2–4.
b. y=–x3+3×2.
c. y=13×3+2×2+4x.

GIẢI:

a. Tập xác định: D=R.
Chiều biến thiên:
Ta có: y′=–3×2+6x =–3x(x–2).
y′=0 ⇔–3x(x–2)=0 ⇔x=0 hoặc x=2.
Hàm số nghịch biến trên các khoảng (–∞;0) và (2;+∞), đồng biến trên khoảng (0;2).
Hàm số đạt cực đại tại điểm x=2, giá trị cực đại của hàm số là y(2)=0.
Hàm số đạt cực tiểu tại điểm x=0, giá trị cực tiểu của hàm số là y(0)=−4.
Giới hạn của hàm số tại vô cực: limx→–∞⁡y=+∞, limx→+∞⁡y=–∞.
Bảng biến thiên:

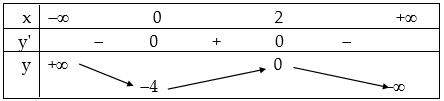
Đồ thị:
Cho x=–1⇒y=0, x=3⇒y=−4.

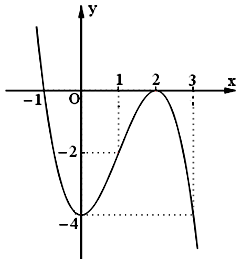
b. Tập xác định: D=R.
Chiều biến thiên:
Ta có: y′=–3×2+6x=–3x(x–2).
y′=0⇔–3x(x–2)=0 ⇔x=0 hoặc x=2.
Hàm số nghịch biến trên các khoảng (–∞;0) và (2;+∞), đồng biến trên khoảng (0;2).
Hàm số đạt cực đại tại điểm x=2, giá trị cực đại của hàm số là y(2)=4.
Hàm số đạt cực tiểu tại điểm x=0, giá trị cực tiểu của hàm số là y(0)=0.
Giới hạn của hàm số tại vô cực: limx→–∞⁡y=+∞, limx→+∞⁡y=–∞.
Bảng biến thiên:

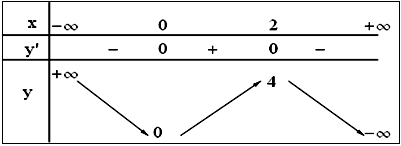
Đồ thị:
Cho x=–1⇒y=4, x=3⇒y=0.

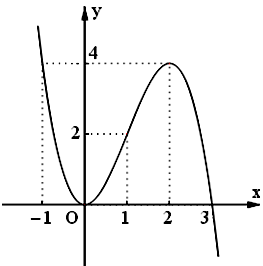
c. Tập xác định: D=R.
Chiều biến thiên:
Ta có: y′=x2+4x+4 =(x+2)2≥0 ∀x∈R.
Hàm số đồng biến trên khoảng (–∞;+∞), hàm số không có cực trị.
Giới hạn của hàm số tại vô cực: limx→–∞⁡y=–∞, limx→+∞⁡y=+∞.
Bảng biến thiên:

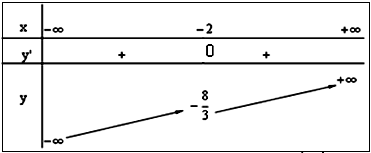
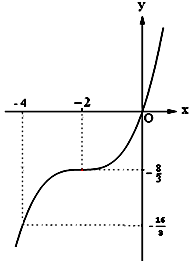
Đồ thị: Cho x=0⇒y=0.

Bài 4:. Cho hàm số y=x3+3×2–mx–4, trong đó m là tham số.
a. Khảo sát sự biến thiên và vẽ đồ thị của hàm số đã cho với m=0.
b. Với giá trị nào của m thì hàm số nghịch biến trên khoảng (–∞;0).

GIẢI:

a. Khi m=0 thì hàm số là: y=x3+3×2–4.
Tập xác định: D=R.
Chiều biến thiên:
Ta có: y′=3×2+6x=3x(x+2).
y′=0⇔3x(x+2)=0 ⇔x=0 hoặc x=–2.
Hàm số đồng biến trên các khoảng (–∞;–2) và (0;+∞), nghịch biến trên khoảng (–2;0).
Hàm số đạt cực đại tại điểm x=–2, giá trị cực đại của hàm số là y(–2)=0.
Hàm số đạt cực tiểu tại điểm x=0, giá trị cực tiểu của hàm số là y(0)=–4.
Giới hạn của hàm số tại vô cực: limx→–∞⁡y=+∞, limx→+∞⁡y=–∞.
Bảng biến thiên:

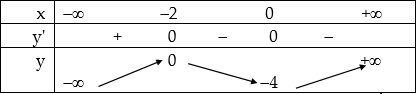
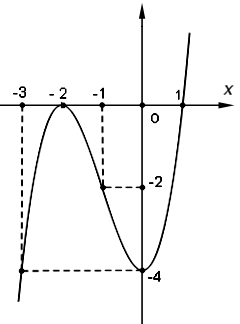
Đồ thị:
Cho x=–3⇒y=–4, x=1⇒y=0.

b. Hàm số y=x3+3×2–mx–4 đồng biến trên khoảng (–∞;0).
⇔y′=3×2+6x–m≥0, ∀x∈(–∞;0).
Xét: g(x)=3×2+6x–m, x∈(–∞;0).
g′(x)=6x+6 ⇒g′(x)=0⇔x=–1.
Bảng biến thiên:

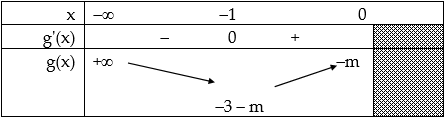
Nhìn vào bảng biến thiên ta thấy:
y′=g(x)=3×2+6x–m≥0, ∀x∈(–∞;0) ⇔–3–m≥0⇔m≤–3.
Vậy khi m≤–3 thì yêu cầu của bài toán được thỏa mãn.

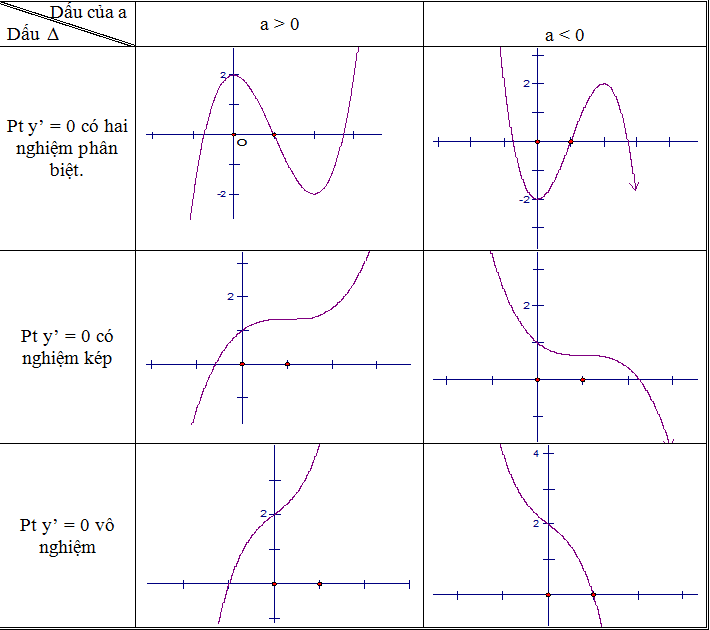
Bài 5: Cho hàm số . Xét 4 đồ thị sau:

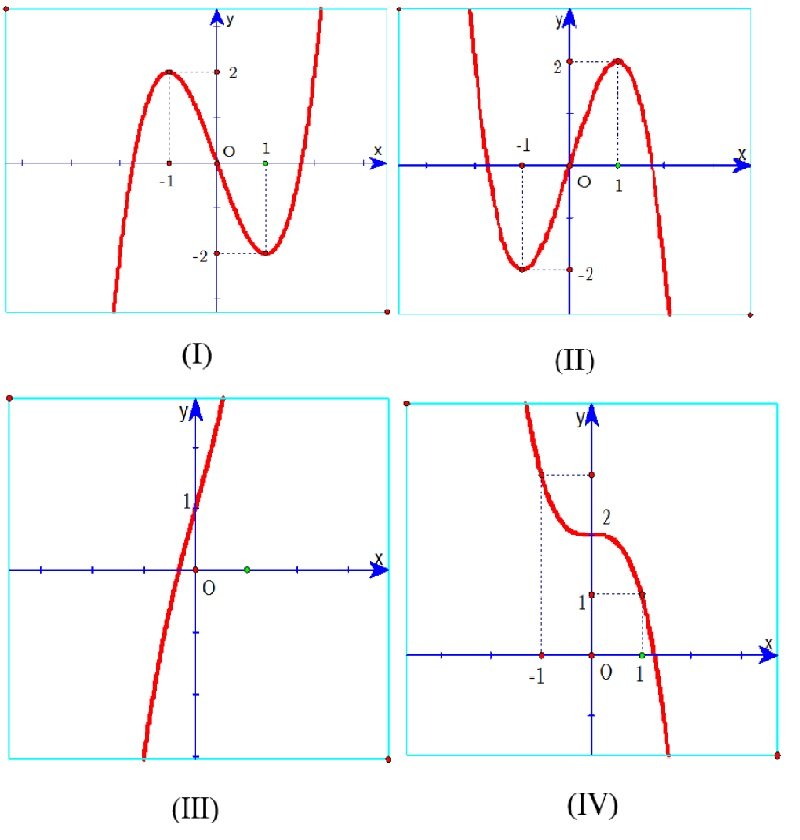
Hãy lựa chọn mệnh đề chính xác:

Khi a>0 và f’(x)=0 có nghiệm kép, đồ thị hàm số sẽ là (IV).Khi a khác 0 và f’(x)=0 tồn tại hai nghiệm phân biệt thì đồ thị (II) xảy ra.Đồ thị (I) khi aĐồ thị (III) khi a>0 và f’(x)=0 vô nghiệm.

Hướng dẫn:

Đồ thị (I) khi a>0, vậy loại C.

Bài 6: Hãy tìm hàm số có đồ thị là hình dưới đây:

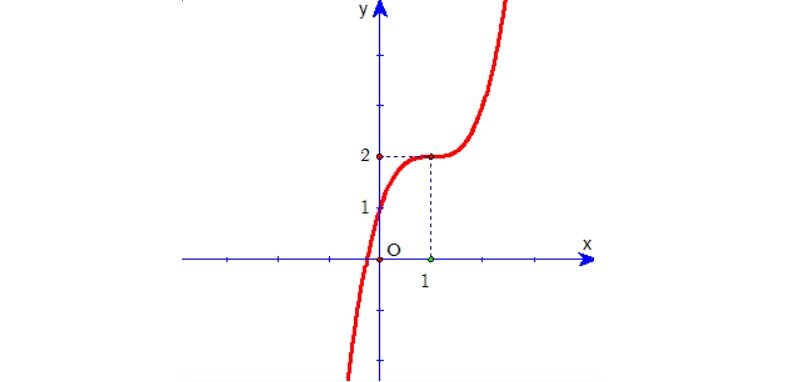
y=x3-3x+1y=-x3+3×2+1y=-x3+x2+3y=x3-3×2+3x+1

Hướng dẫn:

Dựa vào dạng đồ thị, ta có a>0. Hiển nhiên B, C bị loại.

Hàm số này không có cực trị, nên loại đáp án A.

Vậy đáp án D đúng.

Vậy là các bạn vừa được theo dõi cách khảo sát và vẽ đồ thị hàm số bậc ba chi tiết. Hi vọng, bài viết đã mang đến cho bạn thêm nhiều nguồn tư liệu hữu ích. Cách vẽ đồ thị hàm số bậc hai cũng đã được Mầm Non Ánh Dương chia sẻ rất chi tiết. Các bạn tìm hiểu thêm nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục