Cách viết phương trình đường tròn đi qua 3 điểm không thẳng hàng & bài tập

Cách viết phương trình đường tròn đi qua 3 điểm không thẳng hàng là một trong những dạng toán cơ bản về dạng toán đường tròn. Nhằm giúp các em củng cố thêm phần kiến thức Hình học vô cùng quan trọng này, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Bạn tìm hiểu nhé !

I. LÝ THUYẾT VỀ PHƯƠNG TRÌNH ĐƯỜNG TRÒN

This post: Cách viết phương trình đường tròn đi qua 3 điểm không thẳng hàng & bài tập

1. Lập phương trình đường tròn có tâm và bán kính cho trước

Phương trình đường tròn có tâm I(a;b), bán kính R là :

(x−a)²+(y−b)²=R²

2. Nhận xét

Phương trình đường tròn (x−a)²+(y−b)²=R²có thể được viết dưới dạng

x²+y²−2ax−2by+c=0

trong đó c=a²+b²−R²

Ngược lại, phương trình x²+y²−2ax−2by+c=0 là phương trình của đường tròn (C) khi và chỉ khi a²+b²−c>0. Khi đó đường tròn(C) có tâm I(a;b) và bán kính R=√a²+b²−c

3. Phương trình tiếp tuyến của đường tròn

Cho điểm M₀(x₀;y₀)nằm trên đường tròn (C) tâm I(a;b).Gọi Δ là tiếp tuyến với (C) tại M₀

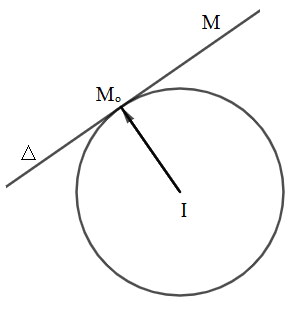
wj8p5hb2ftgmpljaaaaaelftksuqmcc-1-1

Ta có M₀thuộc Δ và vectơ IM₀=(x₀−a;y₀−b) là vectơ pháp tuyến cuả Δ

Do đó Δ có phương trình là:

(x₀−a)(x−x₀)+(y₀−b)(y−y₀)=0

Phương trình này là phương trình tiếp tuyến của đường tròn (x−a)²+(y−b)²=R²tại điểm M₀ nằm trên đường tròn.

III. CÁCH VIẾT PHƯƠNG TRÌNH ĐƯỜNG TRÒN ĐI QUA 3 ĐIỂM KHÔNG THẲNG HÀNG

Giả sử cho đường tròn (C) và 3 điểm không thẳng hàng A, B, C. Viết phương trình đường tròn đi qua 3 điểm A, B và C

CÁCH 1:

Bước 1: Gọi phương trình đường tròn (C) có dạng: x²+y²−2ax−2by+c=0 với a²+b²−c >0

Bước 2: Thay tọa độ của 3 điểm A, B, C vào phương trình đường tròn (C) ta được một hệ 3 phương trình ẩn a, b và c

Bước 3: Giải hệ trên ta được a, b và c.

Bước 4: Thay a, b và c vừa tìm được ở bước 3 vào phương trình đường tròn (C) đã gọi ở trên ta sẽ được phương trình đường tròn (C) cần tìm.

CÁCH 2:

Bước 1: Gọi tâm đường tròn là điểm I(a;b). Vì 3 điểm A, B và C thuộc đường tròn nên ta có:IA=IB=IC. Từ đây ta cũng có hệ phương trình sau:

IA²= IB²

IA²= IC²

Bước 2: Các bạn giải hệ phương trình trên cũng được tọa độ của tấm I

Bước 3: Tìm bán kính R = IA = IB = IC

Bước 4: Thay tọa độ điểm I và bán kính R vào phương trình đường tròn dạng: (x−a)²+(y−b)²=R²

Đối với cách 2 này cũng tương tự như cách 1.

Viết phương trình đường tròn đi qua 3 điểm không thẳng hàng A, B và C có thể phát biểu thành bài toán viết phương trình đường tròn

CÁCH 3:

Ngoại tiếp tam giác ABC. Như vậy ta có thêm một cách phát biểu bài toán nữa và từ đây ta sẽ có thêm một cách viết phương trình đường tròn đi qua 3 điểm không thẳng hàng.

Gọi phương trình đường tròn dạng: (x−a)²+(y−b)²=R²

Bước 1: Tìm tọa độ trung điểm của hai trong 3 cạnh tam giác, giả sử là AB và BC

Bước 2: Viết phương trình đường trung trực của đoạn thẳng AB và

Bước 3: Tìm tọa độ giao điểm của 2 đường trung trực trên, giả sử là điểm I. Khi đó I chính là tâm đường tròn đi qua 3 điểm A, B và C.

Bước 4: Tìm bán kính R = IA = IB = IC

Bước 5: Thay tọa độ tâm I và bán kính R vào phương trình đường tròn .

Chú ý: Tâm đường tròn ngoại tiếp tam giác là giao điểm của 3 đường tung trực trong tam giác. Chúng ta xác định 2 đường trung trực là đủ rồi..

III. MỘT SỐ BÀI TẬP VỀ PHƯƠNG TRÌNH ĐƯỜNG TRÒN

Bài 1. Viết phương trình đường tròn có tâm I và đi qua điểm A, với: dạng 1

a) $mathrm{I}(2 ; 4), mathrm{A}(-1 ; 3)$

b) $mathrm{I}(-3 ; 2), mathrm{A}(1 ;-1)$

c) $mathrm{I}(-1 ; 0), mathrm{A}(3 ;-11)$

d) $mathrm{I}(1 ; 2), mathrm{A}(5 ; 2)$

Bài 2. Viết phương trình đường tròn có tâm I và tiếp xúc với đường thẳng $Delta$ với dạng 2

a) $I(3 ; 4), Delta: 4 x-3 y+15=0$

b) $I(2 ; 3), Delta: 5 x-12 y-7=0$

c) $I(-3 ; 2), Delta equiv O x$

d) $I(-3 ;-5), Delta equiv O y$

Bài 3. Viết phương trình đường tròn có đường kính AB, với: (dạng 3)

a) $mathrm{A}(-2 ; 3), mathrm{B}(6 ; 5)$

b) $mathrm{A}(0 ; 1), mathrm{C}(5 ; 1)$

c) $mathrm{A}(-3 ; 4), mathrm{B}(7 ; 2)$

d) $mathrm{A}(5 ; 2), mathrm{B}(3 ; 6)$

Bài 4. Viết phương trình đường tròn đi qua hai điểm A, B và có tâm I nằm trên đường thẳng, với: (dạng 4)

a) $A(2 ; 3), B(-1 ; 1), Delta: x-3 y-11=0$

b) $A(0 ; 4), B(2 ; 6), Delta: x-2 y+5=0$

c) $A(2 ; 2), B(8 ; 6), Delta: 5 x-3 y+6=0$

Bài 5. Trong các phương trình sau, phương trình nào là phương trình dường tròn. Tìm tâm và bán kinh của đường tròn đó:

a) $x^{2}+y^{2}-2 x-2 y-2=0$

b) $x^{2}+y^{2}-6 x+4 y-12=0$

c) $x^{2}+y^{2}+2 x-8 y+1=0$

d) $x^{2}+y^{2}-6 x+5=0$

e) $16 x^{2}+16 y^{2}+16 x-8 y=11$

f) $7 x^{2}+7 y^{2}-4 x+6 y-1=0$

g) $2 x^{2}+2 y^{2}-4 x+12 y+11=0$ $x^{2}+y^{2}-6 x+2 y ln m+3 ln m+7=0$

h) $4 x^{2}+4 y^{2}+4 x-5 y+10=0$

Bài 6. Tìm m để các phương trình sau là phương trình đường tròn

a) $x^{2}+y^{2}+4 m x-2 m y+2 m+3=0$

b) $x^{2}+y^{2}-2(m+1) x+2 m y+3 m^{2}-2=0$

c) $x^{2}+y^{2}-2(m-3) x+4 m y-m^{2}+5 m+4=0$

d) $x^{2}+y^{2}-2 m x-2left(m^{2}-1right) y+m^{4}-2 m^{4}-2 m^{2}-4 m+1=0$

Bài 7. {*} Tìm m đề các phương trình sau là phương trình đường tròn:

a) $x^{2}+y^{2}-6 x+2 y ln m+3 ln m+7=0$

b) $x^{2}+y^{2}-2 x+4 y+ln (m-2)+4=0$

c) $x^{2}+y^{2}-2 e^{2 m} x+2 e^{m} y+6 e^{2 m}-4=0$

d) $x^{2}+y^{2}-2 x cos m+4 y+cos ^{2} m-2 sin m+5=0$

e) $x^{2}+y^{2}-4 x cos m+2 y sin m-4=0$

Vậy là các bạn vừa được tìm hiểu về cách viết phương trình đường tròn đi qua 3 điểm không thẳng hàng. Hi vọng, đây là nguồn tư liệu hữu ích phục vụ quá trình học tập, giúp các em học tốt hơn. Xem thêm chuyên đề về phương trình đường tròn tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục