Cách tính tích phân của hàm phân thức hữu tỉ nhanh nhất & bài tập
Chuyên đề tích phân là chuyên đề chủ đạo của chương trình Toán 12 nhưng hơi phức tạp. Nếu bạn muốn nắm chắc hơn các công thức tính tích phân hãy theo dõi các bài viết của Mầm Non Ánh Dương nhé ! Ở bài trước chúng tôi đã chia sẻ phương pháp tích phân từng phần, bài viết này các bạn sẽ được tìm hiểu cách tính tích phân của hàm phân thức hữu tỉ nhanh nhất.
I. LÝ THUYẾT CHUNG
This post: Cách tính tích phân của hàm phân thức hữu tỉ nhanh nhất & bài tập
1. Hàm phân thức hữu tỉ là gì?
Một hàm một biến được gọi là một hàm phân thức khi và chỉ khi nó có thể viết được dưới dạng
Trong đó 
và 
là các đa thức đối với 
và không phải là một đa thức không. Tập xác định của 
là tập hợp các điểm mà tại đó mẫu thức
khác 0.
Tất cả các đa thức đều là phân thức với 
. Một hàm số không viết được dưới dạng trên thì không phải là một phân thức (ví dụ, f(x)=sin(x)}
).
Một biểu thức có dạng 
được gọi là một biểu thức phân thức. Trong đại số trừu tượng, 
không bắt buộc là biến số.
Một phương trình phân thức là một phương trình trong đó hai biểu thức phân thức bằng nhau. Các biểu thức đó cũng phải tuân theo các quy tắc trong phân số. Phương trình này có thể được giải bằng luật ba.
2. Các dạng tích phân cơ bản
– Đến đây, có nhiều cách giải. Có thể đặt x = tan(t) để đưa về dạng lượng giác hoặc dùng công thức tích phân từng phần để thu được hệ thức truy hồi. Bạn đọc tự giải tiếp.
Sau khi đã làm thành thạo các dạng tích phân cơ bản trên (các bạn có thể tự đặt ra đề toán để luyện tập và kiểm tra lại bằng máy tính), chúng ta sử dụng các phương pháp thêm bớt để đưa tất cả các bài tích phân hàm phân thức hữu tỉ trở về một trong 4 dạng đã biết cách làm. Phương pháp được trình bày như sau:
II. CÁCH TÍNH TÍCH PHÂN CỦA HÀM PHÂN THỨC HỮU TỈ
Bài toán: Tính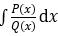 
. Trong đó P(x) và Q(x) là các đa thức theo biến x có bậc lần lượt là m và n.
• Trường hợp 1: m ≥ n.
Lấy P(x) chia cho Q(x) để đưa về các nguyên hàm cơ bản.
• Trường hợp 2: m < n. Phương pháp hệ số bất định
Bước 1: Đưa Q(x) về dạng Q(x)=(ax+b) (cx+d)n(px2+qx+r)
(Trong đó px2+qx+r=0 vô nghiệm).
Bước 2: Đặt
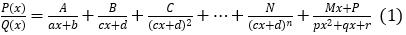
Bước 3: Quy đồng mẫu và đồng nhất hệ số của (1) để tìm các giá trị A, B, C, …, M, N, P.
Một số trường hợp đặc biệt:
a) Bậc của P(x) nhỏ hơn bậc của Q(x) 1 đơn vị (m=n-1).
Thử đặt t = Q(x) và tính dt.
• Nếu dt = k. P(x)dx thì sử dụng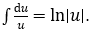 
• Nếu dt ≠ k. P(x)dx thì sử dụng phương pháp hệ số bất định.
b) Tích phân dạng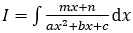 
:
• Nếu ax2+bx+c=0 có 2 nghiệm phân biệt thì sử ta sử dụng phương pháp hệ số bất định.
• Nếu ax2+bx+c=0 có nghiệm kép x=x0 thì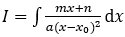 
, sau đó đặt t=x-x0.
• Nếu ax2+bx+c=0 vô nghiệm thì ta sử dụng phương pháp lượng giác hoá.
c) Một số nguyên hàm cần nhớ:
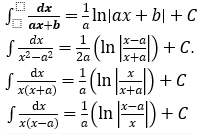
VÍ DỤ:
III. BÀI TẬP TÍNH TÍCH PHÂN CỦA HÀM PHÂN THỨC HỮU TỈ
Bài 1: Tính tích phân
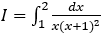
Hướng dẫn:
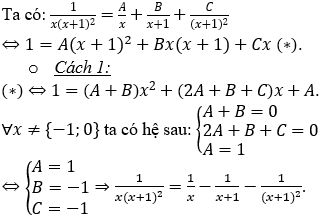
Bài 2: Tính tích phân
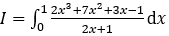
Hướng dẫn:
Bài 3: Tính tích phân
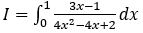
Hướng dẫn:
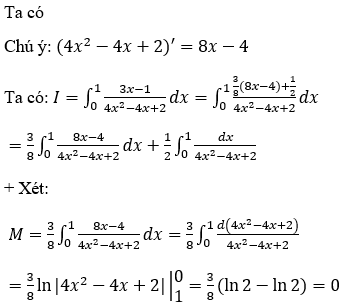
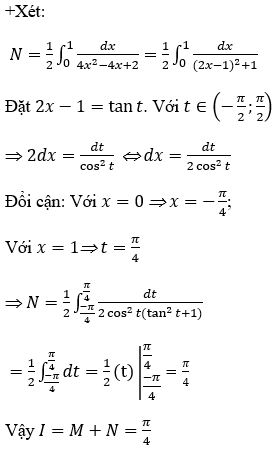
Bài 4: Tính tích phân
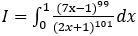
Hướng dẫn:
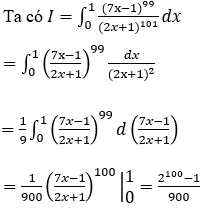
Bài 5: Tính tích phân
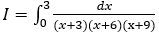
Hướng dẫn:
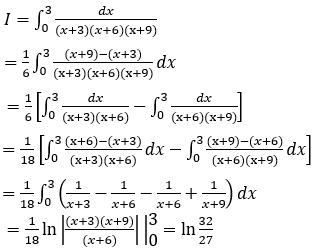
Bài 6: Tính tích phân
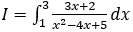
Hướng dẫn:
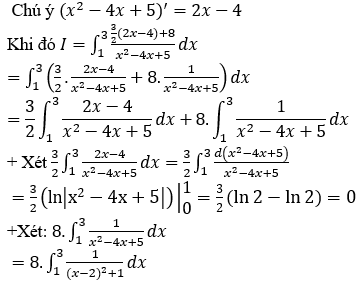
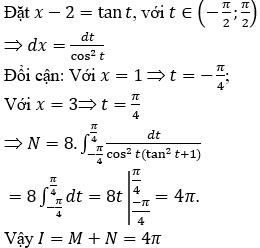
Bài 7: Tính tích phân
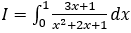
Hướng dẫn:
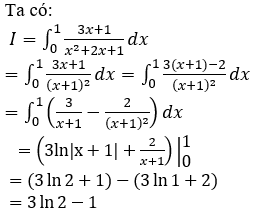
Bài 8: Tính tích phân
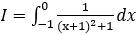
Hướng dẫn:
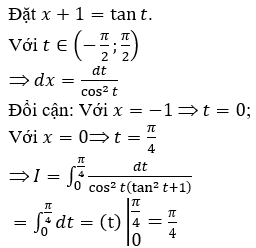
Trên đây Mầm Non Ánh Dương đã chia sẻ đến quý thầy cô và các bạn học sinh Cách tính tích phân của hàm phân thức hữu tỉ hay nhất và bài tập vận dụng. Hi vọng, đây sẽ nguồn tư liệu thiết yếu giúp các bạn dạy và học tốt hơn. Cảm ơn các bạn đã đồng hành cùng bài viết ! Xem thêm phương pháp tích phân từng phần nữa bạn nhé !
Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục
