Tìm hiểu cách tính độ dài Vectơ, khoảng cách giữa hai điểm trong hệ tọa độ

Tìm hiểu cách tính độ dài Vectơ, khoảng cách giữa hai điểm trong hệ tọa độ

Lý thuyết về Vectơ cũng như cách tính độ dài Vectơ, khoảng cách giữa hai điểm trong hệ tọa độ học sinh đã được tìm hiểu trong chương trình Toán 10. Bài viết hôm nay, Mầm Non Ánh Dương sẽ hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này. Bạn tìm hiểu để có thêm nguồn tư liệu quý phục vụ quá trình dạy và học nhé !

I. LÝ THUYẾT CẦN GHI NHỚ

This post: Tìm hiểu cách tính độ dài Vectơ, khoảng cách giữa hai điểm trong hệ tọa độ

II. CÁCH TÍNH ĐỘ DÀI VECTƠ, KHOẢNG CÁCH GIỮA HAI ĐIỂM TRONG HỆ TỌA ĐỘ

1. Phương pháp giải

Độ dài vecto

– Định nghĩa: Mỗi vecto đều có một độ dài, đó là khoảng cách giữa điểm đầu và điểm cuối của vecto đó. Độ dài của vecto 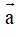 được ký hiệu là ||.

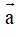Do đó đối với các vectơ 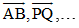 ta có:

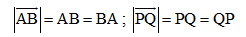
– Phương pháp: muốn tính độ dài vectơ, ta tính độ dài cách giữa điểm đầu và điểm cuối của vectơ.

– Trong hệ tọa độ: Cho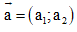 

Độ dài vectơ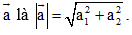 

Khoảng cách giữa hai điểm trong hệ tọa độ

Áp dụng công thức sau

Trong mặt phẳng tọa độ, khoảng cách giữa hai điểm M(x_M;y_M) và N(x_N;y_N) là

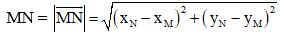
2. Ví dụ minh họa

Ví dụ 1: Trong mặt phẳng tọa độ Oxy, cho hai vectơ =(4;1) và 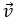=(1;4). Tính độ dài vectơ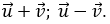 

Hướng dẫn giải:

Ta có:

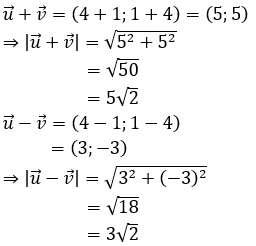
Ví dụ 2: Trong mặt phẳng tọa độ Oxy, cho tam giác ABC có A(1; 4), B(3; 2), C(5; 4). Chu vi P của tam giác đã cho.

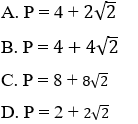
Hướng dẫn giải:

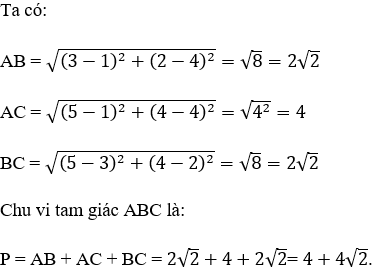
Đáp án B

Ví dụ 3: Trong mặt phẳng tọa độ Oxy, tính khoảng cách giữa hai điểm M(1; -2) và N (-3; 4).

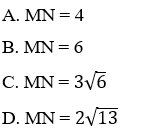
Hướng dẫn giải:

Đáp án D

Ví dụ 4: Trong mặt phẳng tọa độ Oxy, cho bốn điểm A(-1; 1), B(0; 2), C(3; 1) và D(0; -2). Khẳng định nào sau đây là đúng?

A. Tứ giác ABCD là hình bình hành

B. Tứ giác ABCD là hình thoi

C. Tứ giác ABCD là hình thang cân

D. Tứ giác ABCD không nội tiếp được đường tròn

Hướng dẫn giải:

Từ (1) và (2) suy ra ABCD là hình thang cân (hình thang có hai đường chéo bằng nhau là hình thang cân).

Đáp án C

III. BÀI TẬP VẬN DỤNG

Bài 1: Gọi A’, B’, C’ lần lượt là trung điểm của các cạnh BC, CA, AB của tam giác ABC. Tính | + |

A. AA’

B. BB’

C. CC’

D. AA’ + BB’ + CC’

Bài 2: Cho hình vuông ABCD cạnh a. |++ | bằng

A. 2a

B. a√2

C. 0

D.2a√2

Bài 3: Cho tam giác ABC vuông tại A có AB= √5 ,AC=2√5.

a) Độ dài vectơ  +  bằng:

A. √5

B. 5√5

C. 25

D. 5

b) Độ dài vectơ  –  bằng:

A. √5

B. 15

C. 5

D. 2

Bài 4: Cho tam giác ABC. Vectơ + có giá chứa đường thẳng nào sau đây?

A. Tia phân giác của góc A

B. Đường cao hạ từ đỉnh A của tam giác ABC

C. Đường trung tuyến qua A của tam giác ABC

D. Đường thẳng BC

Bài 5: Cho tam giác ABC vuông tại A và AB = 3, AC = 8. Vectơ + có độ dài là:

A. 4

B. 5

C. 10

D.8

Bài 6: Cho hình thang có hai đáy là AB = 3a và CD = 6a. Khi đó | + | bằng bao nhiêu?

A. 9a

B. 3a

C. – 3a

D. 0

Trên đây Mầm Non Ánh Dương đã giới thiệu đến các bạn lý thuyết về Vectơ và cách tính độ dài Vectơ, khoảng cách giữa hai điểm trong hệ tọa đ hay. Hi vọng, đây sẽ là nguồn tư liệu thiết yếu giúp các bạn dạy và học tốt hơn. Xem thêm cách tìm Vectơ chỉ phương của đường thẳng tại đường link này bạn nhé !

Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục