Tìm hiểu cách giải phương trình bậc ba nhanh chóng, chính xác

Lý thuyết về phương trình bậc ba cũng như cách giải phương trình bậc ba nhanh chóng, chính xác không phải học sinh nào cũng nắm vững, mặc dù đây là một trong những phần kiến thức trọng tâm của chương trình Toán 9, phân môn Đại số. Bài viết hôm nay, Mầm Non Ánh Dương sẽ giúp bạn hệ thống lại các kiến thức cần ghi nhớ về chuyên đề này và cách giải phương trình bậc ba cực hay nhé !

I. LÝ THUYẾT VỀ PHƯƠNG TRÌNH BẬC BA

This post: Tìm hiểu cách giải phương trình bậc ba nhanh chóng, chính xác

Phương trình bậc ba được đề cập lần đầu tiên bởi nhà toán học Ấn Độ cổ Jaina khoảng giữa năm 400 TCN và 200 CN.

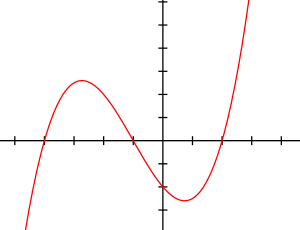
6evfg4trzsx6igx7z5wwkv1tk131jlgj3veqxwzi-1

Phương trình bậc ba được đề cập lần đầu tiên bởi nhà toán học Ấn Độ cổ Jaina khoảng giữa năm 400 TCN và 200 CN. Hiểu đơn giản, phương trình bậc ba là phương trình có ẩn số mũ 3 (tức bậc ba). Các dạng phương trình bậc ba thường thấy gồm:

${displaystyle x^{3}+mx+n}$
${displaystyle x^{3}+mx^{2}+n}$
ax³ + bx² + cx + d

II. CÁC CÁCH GIẢI PHƯƠNG TRÌNH BẬC BA CỰC HAY

1. Phương pháp Cardano

Phương pháp thiên về việc đặt ẩn phụ và khá phức tạp. Tuy nhiên lợi thế của phương pháp này là giải quyết hầu hết các bài tập phương trình bậc ba mà không cần quan tâm đến hệ số cũng như kết quả nghiệm xấu hay là đẹp. Đây là phương pháp giải được cho là tổng quát nhất và cũng khá là phức tạp:

Xét phương trình bậc 3: x³+ax²+ bx + c= 0 (1)

Đặt thì phương trình (1) luôn biến đổi về dạng chính tắc là: y³ +py + q = 0 trong đó trường hợp này ta sẽ xét, còn trường hợp bằng 0 đơn giản hơn rất nhiều.

VÍ DỤ MINH HỌA

Ví dụ 1: giải phương trình x³+ x²+x=-1/3

ugs9by0zgbfamnehjh3ccssl01zwx4g7wefvxgpy

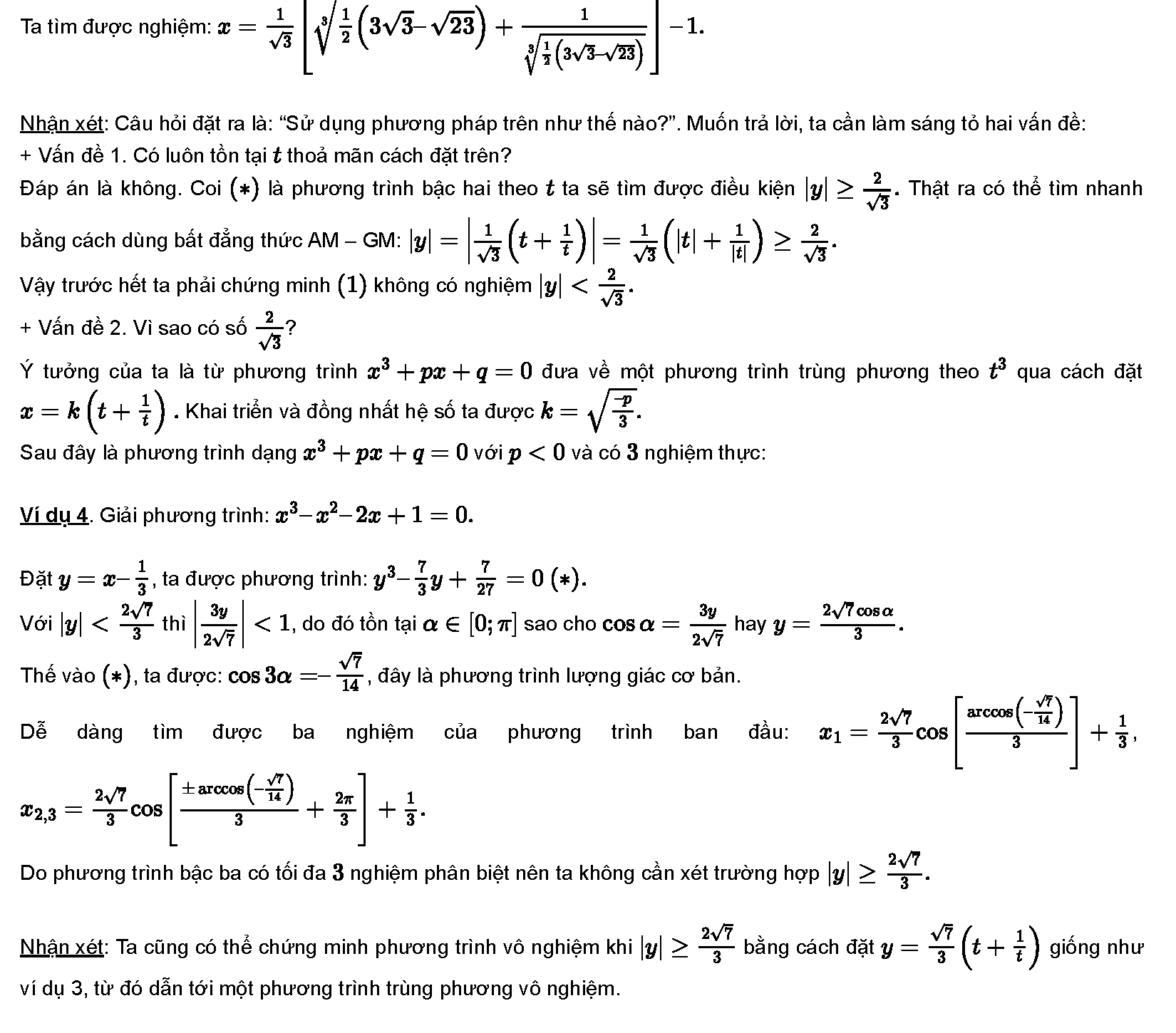
jhvriigzf6ljc8x63pxwz07g8mu9mis3wwrcy8jb

dobpkgqfknfq1ha34n28c1oajpn9iyfrdkenxueg

uency3edqfrrg4ayxdirv9agi3fi65ygwssstho2

2. Phương pháp phân tích thành nhân tử

Đây là phương pháp khá đơn giản tuy nhiên điều kiện của phương trình phải là có nghiệm đẹp. Nghiệm đẹp ở đây có thể là số nguyên hoặc là phân số. Sau khi tìm được nhân tử chung thứ nhất thì việc còn lại chỉ là giải một phương trình bậc hai vô cùng đơn giản

Khi một phương trình bậc 3 có nghiệm <x=r> thì chắc chắn nó sẽ xuất hiện nhân tử. Sau khi tìm được nghiệm chung, ta tiến hành phân tích thành nhân tử qua các bước sau:

Bước 1: Tìm nghiệm đơn giản của phương trình. Đối với các bài toán này thường có nghiệm khá đơn giản như 0,1,2,3. Nếu phức tạp hơn một tí thì có thể dùng máy tính casio để nhẩm nghiệm với chức năng solve

Bước 2: Sau khi có nghiệm, ta tiến hành phép phân tích phân tử bằng cách chia tách các hệ số, sơ đồ hoocne hoặc phương pháp đồng nhất thức đề được cả.

3. Phương pháp lượng giác hóa

Đặt các giá trị:

${displaystyle Delta =b^{2}-3ac}$

${displaystyle k={frac {9abc-2b^{3}-27a^{2}d}{2{sqrt {|Delta |^{3}}}}}qquad (Delta neq 0)}$

1) Nếu {displaystyle Delta >0}

1.1)

: Phương trình có ba nghiệm

${displaystyle x_{1}={frac {2{sqrt {Delta }}cos left({frac {arccos(k)}{3}}right)-b}{3a}}}$

${displaystyle x_{2}={frac {2{sqrt {Delta }}cos left({frac {arccos(k)}{3}}-{frac {2pi }{3}}right)-b}{3a}}}$

${displaystyle x_{3}={frac {2{sqrt {Delta }}cos left({frac {arccos(k)}{3}}+{frac {2pi }{3}}right)-b}{3a}}}$

1.2)

: Phương trình có một nghiệm duy nhất

${displaystyle x={frac {{sqrt {Delta }}|k|}{3ak}}left({sqrt[{3}]{|k|+{sqrt {k^{2}-1}}}}+{sqrt[{3}]{|k|-{sqrt {k^{2}-1}}}}right)-{frac {b}{3a}}}$

2) Nếu {displaystyle Delta =0} :

2.1) { ${displaystyle b^{3}-27a^{2}d=0}$ : Phương trình có một nghiệm bội

${displaystyle x={frac {-b}{3a}}}$

2.2) ${displaystyle b^{3}-27a^{2}dneq 0}$ : Phương trình có một nghiệm duy nhất

${displaystyle x={frac {-b+{sqrt[{3}]{b^{3}-27a^{2}d}}}{3b}}}$

3) Nếu {displaystyle Delta <0} : Phương trình có một nghiệm duy nhất

${displaystyle x={frac {sqrt {|Delta |}}{3a}}left({sqrt[{3}]{k+{sqrt {k^{2}+1}}}}+{sqrt[{3}]{k-{sqrt {k^{2}+1}}}}right)-{frac {b}{3a}}}$

III. BÀI TẬP VỀ PHƯƠNG TRÌNH BẬC BA

Bài 1: Giải phương trình x³−12x+16=0

Giải:

Cách 1:

Dễ thấy x=2 là một nghiệm của đa thức f(x)=x³−12x+16 nên ta chia f(x) cho (x−2) để được: f(x)=(x−2)(x²+2x−8).

Và đưa phương trình đã cho về:
(x−2)(x2+2x−8)=0

⇔x−2=0 và x²+2x−8=0

⇔x=2 và x=−4.

Cách 2:

x³−12x+16=0

⇔x³−4x−8x+16=0

⇔x(x²−4)−8(x−2)=0

⇔ (x−2) [ x(x+2)−8] =0

⇔(x−2)(x+2x−8)=0

⇔(x−2)(x−2)(x+4)=0

⇔x=2 và x=−4.

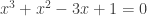
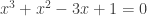
Bài 2: Giải phương trình $x^3 + x^2 - 3x + 1 = 0$

$x^3 + x^2 - 3x + 1 = 0$

$Leftrightarrow (x - 1)(x^2 + 2x - 1) = 0$

$Leftrightarrow x - 1 = 0,,,vee ,,, x^2 + 2x - 1 = 0$

$Leftrightarrow x = 1 ,,,vee ,,, x = -1 pm sqrt{2}$

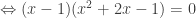
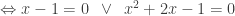
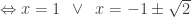
Vậy phương trình có tập hợp nghiệm là 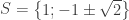$S = begin{Bmatrix}1; -1 pm sqrt{2}end{Bmatrix}$

Vậy là các bạn đã được tìm hiểu cách giải phương trình bậc ba nhanh chóng, chính xác và các dạng bài tập thường gặp. Hi vọng, bài viết đã mang lại cho bạn những kiến thức bổ ích. Xem thêm cách giải phương trình chứa ẩn ở mẫu tạp đường link này nữa bạn nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục