Số hữu tỉ là gì ? Các tính chất của số hữu tỉ và các dạng bài tập
Bài viết hôm nay, Mầm Non Ánh Dương sẽ giới thiệu cùng các bạn chuyên đề Số hữu tỉ là gì ? Các tính chất của số hữu tỉ và các dạng bài tập. Phần kiến thức này học sinh đã được tìm hiểu trong chương trình Toán 7, phân môn Đại số. Đây là phân kiến thức trọng tâm của chương trình. Các bạn hãy chia sẻ bài viết sau đây để nắm chắc hơn nhé !
I. SỐ HỮU TỈ LÀ GÌ?
This post: Số hữu tỉ là gì ? Các tính chất của số hữu tỉ và các dạng bài tập
1. Khái niệm:
Số hữu tỉ là các số x có thể biểu diễn dưới dạng phân số a/b, trong đó a và b là các số nguyên với b # 0
Tập hợp các số hữu tỉ, hay còn gọi là trường số hữu tỉ ký hiệu là Q (chữ đậm) hoặc ℚ (chữ viền).

2. Ví dụ
Ví dụ 1:
Ta có thể viết:
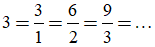
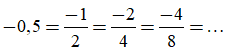
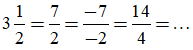
Ví dụ 2:
Các số hữu tỉ ví dụ như:
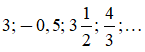
Ví dụ 3:
Các số hữu tỉ ví dụ như:
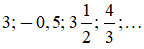
thì kí hiệu như sau:
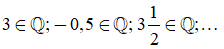
3. So sánh hai số hữu tỉ
Để so sánh hai số hữu tỉ x, y ta thường làm như sau:
• Viết x, y dưới dạng hai phân số có cùng mẫu dương
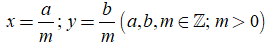
• So sánh hai số nguyên a và b
+ Nếu a < b thì x < y
+ Nếu a = b thì x = y
+ Nếu a > b thì x > y
• Trên trục số nếu x < y thì điểm x nằm bên trái điểm y
• Số hữu tỉ lớn hơn 0 được gọi là số hữu tỉ dương.
• Số hữu tỉ nhỏ hơn 0 được gọc là số hữu tỉ âm.
• Số 0 không phải là số hữu tỉ dương cũng không phải là số hữu tỉ âm.
Nhận xét:
+ Số hữu tỉ a/b là số hữu tỉ dương (a/b > 0) thì a, b cùng dấu.
+ Số hữu tỉ a/b là số hữu tỉ âm (a/b < 0) thì a, b trái dấu.
+ Ta có:
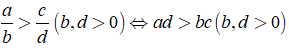
Ví dụ: So sánh hai số hữu tỉ
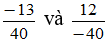
Ta có:
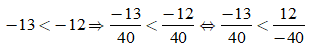
4. Biểu diễn số hữu tỉ trên trục số
Mỗi số hữu tỉ được biểu diễn bởi một điểm trên trục số và không phụ thuộc vào cách chọn phân số xác định nó.
Ví dụ: Số hữu tỉ 2/3 được biểu diễn bởi điểm M trên trục số sau:
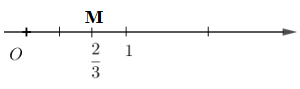
II. CÁC TÍNH CHẤT SỐ HỮU TỈ
Số hữu tỉ có các tính chất sau đây. Bạn tìm hiểu nhé !
1. Nhân số hữu tỉ
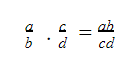
Ví dụ:
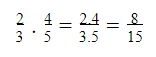
2. Chia số hữu tỉ
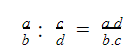
Ví dụ:
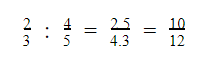
Mỗi số hữu tỉ đều có thể biểu diễn bằng một số thập phân hữu hạn hoặc vô hạn tuần hoàn.
3. Giá trị tuyệt đối của các số hữu tỉ
|x| = x nếu x≥0
|x| = -x nếu x<0
4. Số đối số hữu tỉ
- Số đối của số hữu tỉ là một số hữu tỉ mà tổng của nó với số hữu tỉ này cho kết quả bằng 0.
- Nếu số hữu tỉ là số hữu tỉ âm thì số đối của nó sẽ là số hữu tỉ dương.
- Nếu số hữu tỉ là số hữu tỉ dương thì số đối của nó là một số hữu tỉ âm.
- Lũy thừa của một số hữu tỉ số bằng tích của các lũy thừa.
- Lũy thừa của một tích sẽ bằng tích của các lũy thừa:
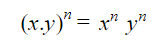
- Lũy thừa của một thương bằng thương của các lũy thừa:
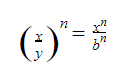
III. BÀI TẬP VỀ SỐ HỮU TỈ
Bài : Tính giá trị của biểu thức
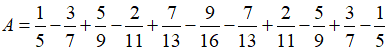

Đáp số: chọn đáp án a
Bài 2:
Cho
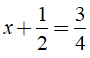
Giá trị của x bằng
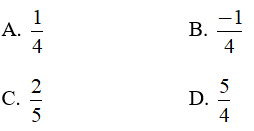
Hướng dẫn giải:
Ta có:
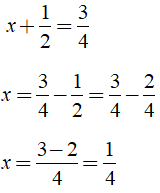
Chọn đáp án A.
Bài 3: Với ba chữ số 1, hãy biểu diễn số hữu tỉ âm lớn nhất và số hữu tỉ âm nhỏ nhất.
Hướng dẫn giải:
+ Số hữu tỉ âm nhỏ nhất là -111
+ Số hữu tỉ âm lớn nhất là -1/11
Bài 4: So sánh các số hữu tỉ sau bằng cách nhanh nhất
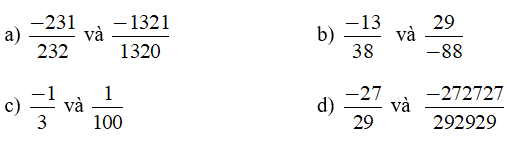
Hướng dẫn giải:
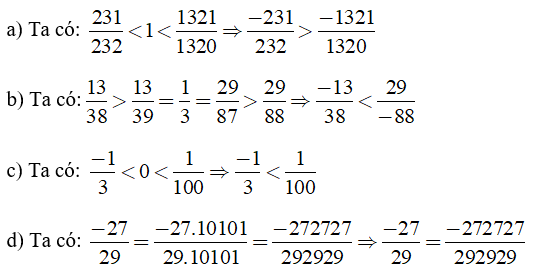
Bài 5:
Tìm x∈Q biết: (23x−15)(35x+23)<0.
Giải:
Ta có: (23x−15)(35x+23)<0
⇔[23(x−310)][35(x+109)]<0
⇔23.35(x−310)(x+910)<0
⇔(x−310)(x+109)<0
Từ đó suy ra: x−310 và x+109 trái dấu, mặt khác ta lại có x−310<x+109
Nên suy ra: x−310<0 và x+109>0⇔−109<x<310.
Vậy các số hữu tỉ x thỏa mãn đề ra là −109<x<310.
Bài 6:
Tìm x biết x∉{1;3;8;20}
và: 2(x−1)(x−3)+5(x−3)(x−8)+12(x−8)(x−20)−1x−20=−34.
Giải:
Ta có: 2(x−1)(x−3)+5(x−3)(x−8)+12(x−8)(x−20)−1x−20
=(x−1)−(x−3)(x−3).(x−1)+(x−3)−(x−8)(x−8).(x−3)+(x−8)−(x−20)(x−20).(x−8)−1x−20.
=1x−3−1x−1+1x−8−1x−3+1x−20−1x−8−−1x−20=−1x−1.
⇒−1x−1=−34⇒x=73.
Bài 7:
Viết 5 số hữu tỉ trên một vòng tròn sao cho trong đó tích hai số cạnh nhau bằng 136. Hãy tìm cách viết đó.
Giải:
Gọi 5 số hữu tỉ đó lần lượt là a1, a2, a3, a4, a5 (các số này đều khác 0)
Ta có: a1a2=a2a3⇒a1=a3
Tương tự có: a2=a4,a3=a5
Mà: a1a2=a5a1⇒a2=a5.
⇒a1=a2=a3=a4=a5=±16.
Bài 8: Thực hiện các phép tính sau:
a) (−35+511):(−37)+(−25+611):(−37)
b) (−25+14:−7101).(5517−47.23).(1−513:513).
Giải:
a) (−35+511):(−37)+(−25+611):(−37)
=(−35+511+−25+611):(−37)
=(−3−25+5+611):(−37) =0:(−37)=0.
b) (−25+14:−7101).(5517−47.23).(1−513:513)
=(−25+14:−7101).(5517−47.23).(1−1)
=(−25+14:−7101).(5517−47.23).0=0.
Bài 9: Tìm x,y,z biết rằng: (x−15)(y+12)(z−3)=0 Và x+1=y+2=z+3.
Giải:
Ta có: (x−15)(y+12)(z−3)=0
⇔x−15=0 hoặc y+12=0 hoặc z−3=0
⇔x=15 hoặc y=−12 hoặc z=3
∙ Nếu x=15, kết hợp với x+1=y+2=z+3 ta suy ra y=−45;z=−95
∙ Nếu y=−12, kết hợp với x+1=y+2=z+3 ta suy ra x=12;z=−32
∙ Nếu z=3, tương tự ta suy ra x=5;y=4
Vậy ta có ba bộ số thỏa mãn đó là:
15;−45;−95 hoặc 12;−12;−32 hoặc 5;4;3.
Bài 10*: a) Cho 13 số hữu tỉ, trong đó tổng của bốn số bất kì nào cũng là một số dương. Chứng minh rằng tổng của 13 số đó là một số dương.
b) Cho 13 số hữu tỉ, trong đó tích của 3 số bất kì nào cũng là một số âm. Chứng minh rằng 13 số đã cho đều là số âm.
Giải:
Giải sử 13 số đã cho lần lượt là: a1;a2;a3;…;a12;a13.
a) Ta xét 13 tổng sau: a1+a2+a3+a4>0
a2+a3+a4+a5>0
a3+a4+a5+a6>0
…..
a13+a1+a2+a3>0.
Cộng các bất đằng thức trên vế theo vế ta được: 4(a1+a2+a3+…+a13)>0.
⇒a1+a2+a3+…+a13>0
Vậy tổng của 13 số đã cho là một số dương.
b) Xét 13 tích sau: a1.a2.a3<0,a2.a3.a4<0,…,a13.a1.a2<0.
Suy ra: (a1.a2.a3…a13)3<0⇒a1.a2.a3…a13<0.
Tách riêng một số từ tích 13 số nói trên, 12 số còn lại chia thành 4 nhóm ba số ta có:
(a1.a2.a3).(a4.a5.a6).(a7.a8.a9).(a10.a11.a12).a13<0.
Ta thấy tích mỗi nhóm ba số là một số âm nên tích của 4 nhóm như vậy là số dương suy ra số được tách riêng ra là một số âm.
Tương tự cho 13 số và ta được 13 số đã cho đều là số âm.
Vậy là Mầm Non Ánh Dương đã chia sẻ đến quý bạn đọc chuyên đề Số hữu tỉ là gì ? Các tính chất của số hữu tỉ và các dạng bài tập vô cùng chi tiết. Hi vọng, sau khi chia sẻ cùng bài viết bạn đã nắm chắc hơn phần kiến thức này. Hãy chia sẻ thêm các quy tắc cộng trừ nhân chia số nguyên tại đường link này nữa bạn nhé !
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục





