Phương pháp tích phân từng phần hay nhất và bài tập vận dụng
Nguyên hàm tích phân là nội dung vô cùng quan trọng trong chương trình Toán 12 xuất hiện nhiều trong các đề thi. Nhằm giúp các em nắm vững hơn phần kiến thức này, Mầm Non Ánh Dương đã chia sẻ phương pháp tích phân từng phần hay nhất và nhiều dạng bài tập vận dụng. Bạn tìm hiểu nhé !
I. LÝ THUYẾT VỀ TÍCH PHÂN TỪNG PHẦN
This post: Phương pháp tích phân từng phần hay nhất và bài tập vận dụng
1. Tích phân từng phần là gì?
Trong vi tích phân nói riêng, và trong giải tích toán học nói chung, tích phân từng phần là quá trình tìm tích phân của tích các hàm dựa trên tích phân các đạo hàm và nguyên hàm của chúng. Nó thường được sử dụng để biến đổi nguyên hàm của tích các hàm thành một nguyên hàm mà đáp án có thể được tìm thấy dễ dàng hơn. Quy tắc có thể suy ra bằng cách tích hợp quy tắc nhân của đạo hàm.
Nếu u = u(x) và du = u′(x) dx, trong đó v = v(x) và dv = v′(x) dx, thì tích phân từng phần phát biểu rằng:
hay gọn hơn:
Có các công thức tổng quát hơn của tích phân từng phần cho tích phân Riemann-Stieltjes và tích phân Lebesgue-Stieltjes. Chuỗi số cũng có mô hình rời rạc tương tự gọi là tổng từng phần.
2. Định lý
Định lý có thể được suy ra như sau. Giả sử u(x) và v(x) là hai hàm khả vi liên tục. Quy tắc nhân phát biểu rằng (theo ký hiệu của Leibniz):
Tích phân cả hai vế đối với x,
sau đó áp dụng định nghĩa của nguyên hàm,
cho ta công thức tích phân từng phần.
Bởi vì du và dv là các vi phân của một hàm một biến x,
Tích phân gốc ∫uv′ dx chứa v′ (đạo hàm của v); để áp dụng định lý, phải tim nguyên hàm v (của v′), và tính tích phân ∫vu′ dx.
II. CÔNG THỨC, CÁCH TÍNH TÍCH PHÂN TỪNG PHẦN
Các bước tính tích phân từng phần:
+ Bước 1: Biến đổi tích phân ban đầu về dạng .
+ Bước 2: Đặt (chọn
 là một nguyên hàm của
là một nguyên hàm của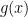 ).
).
+ Bước 3: Khi đó 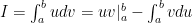 .
.
Thứ tự ưu tiên đặt u: Thứ tự ưu tiên chọn u: Logarit ⟶ đa thức ⟶ Lượng giác = mũ.
Ví dụ:
Cho 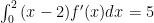 và
và 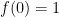 . Tính
. Tính 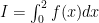 .
.
A. 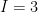 . B.
. B. 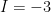 . C.
. C.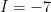 . D.
. D. 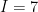 .
.
Lời giải:
Đặt .
Ta có 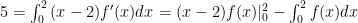
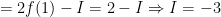 .
.
Chọn B.
III. CÁC DẠNG BÀI TẬP VỀ TÍCH PHÂN TỪNG PHẦN
Bài 1: Tính tích phân sau:
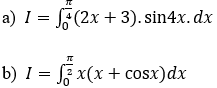
Hướng dẫn:
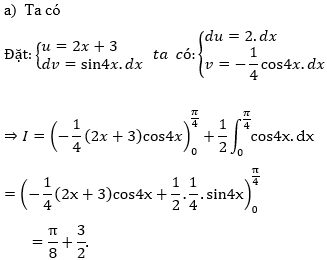
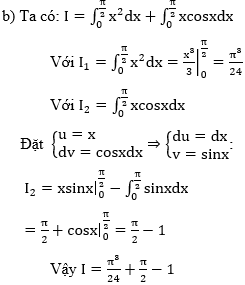
Trên đây Mầm Non Ánh Dương đã chia sẻ đến quý thầy cô và các bạn học sinh phương pháp tích phân từng phần hay nhất và bài tập vận dụng. Hi vọng, đây sẽ nguồn tư liệu thiết yếu giúp các bạn dạy và học tốt hơn. Cảm ơn các bạn đã đồng hành cùng bài viết ! Xem thêm công thức tính tích phân nữa bạn nhé !
Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục





