Lý thuyết hình chữ nhật. Cách chứng minh tứ giác là hình chữ nhật nhanh nhất

Lý thuyết hình chữ nhật. Cách chứng minh tứ giác là hình chữ nhật nhanh nhất

Hình chữ nhật là gì ? Hình chữ nhật có những tính chất gì? Dấu hiệu nhận biết hình chữ nhật ra sao hay cách chứng minh tứ giác là hình chữ nhật thế nào cho hay lại nhanh gọn … Tất cả những mắc mắc này sẽ được Mầm Non Ánh Dương chia sẻ qua bài viết sau đây. Bạn tìm hiểu nhé !

I. LÝ THUYẾT VỀ HÌNH CHỮ NHẬT

This post: Lý thuyết hình chữ nhật. Cách chứng minh tứ giác là hình chữ nhật nhanh nhất

1. Định nghĩa

Hình chữ nhật là tứ giác có bốn góc vuông. Hình chữ nhật cũng là một hình bình hành.

                                   

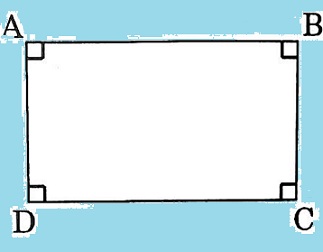
ABCD là hình chữ nhật ⇔ˆA=ˆB=ˆC=ˆD=90∘

Nhận xét: Hình chữ nhật cũng là một hình bình hành cũng là một hình thang cân.

2. Tính chất

 Hình chữ nhật là có tất cả các tính chất của hình bình hành và hình thang cân.

– Hai cạnh đối song song, hai cạnh đối bằng nhau, hai góc đối bằng nhau

– Hai đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường.

3. Dấu hiệu nhận biết

a) Tứ giác có ba góc vuông là hình chữ nhật.

b) Hình thang cân có một góc vuông là hình chữ nhật.

c) Hình bình hành có một góc vuông là hình chữ nhật.

d) Hình bình hành có hai đường chéo bằng nhau là hình chữ nhật.

4. Định lí

a. Định lí 1: Trong Hình chữ nhật, hai đường chéo bằng nhau và cắt nhau tại trung điểm mỗi đường. Ngược lại, nếu tứ giác có 2 đường chéo bằng nhau và cắt nhau tại trung điểm của mỗi đường là hình chữ nhật.

Ví dụ: Cho tứ giác ABCD có AC = BD và cắt nhau tại O, trong đó OA = OB = OC = OD, chứng minh Tứ giác ABCD là Hình chữ nhật.

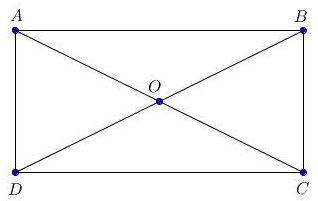
Xét tam giác ABD có:

OA = OB = OD (gt) => ∆ABD vuông tại A

( Tính chất đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền trong tam giác vuông )

Chứng minh tương tự, ta có:

∆ABC vuông tại B, ∆BCD vuông tại C, ∆CDA vuông tại D

=> Tứ giác ABCD là hình chữ nhật do có 4 góc vuông.

b. Định lí 2: Áp dụng vào Tam giác

+ Trong tam giác vuông đường trung tuyến ứng với cạnh huyền bằng nửa cạnh huyền.

+ Nếu một tam giác có đường trung tuyến ứng với một cạnh bằng nửa cạnh ấy thì tam giác đó là tam giác vuông.

Ví dụ: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC, E là điểm đối xứng với H qua I. Chứng minh tứ giác AHCE là hình chữ nhật.

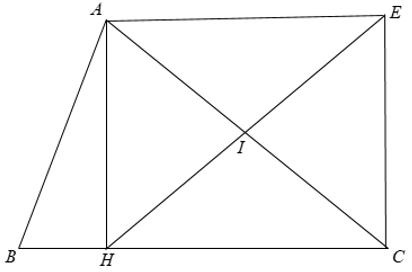
⇒ HE là đường trung tuyến của Δ AHC.

⇒ HI = ½AC = AI = IC.

Mà E đối xứng với H qua I ⇒ HI = IE.

Khi đó ta có HI = IE = AI = IC.

+ Xét Δ HCE có CI là đường trung tuyến ứng với cạnh HE

mà CI = ½ HE ⇒ Δ HCE vuông tại C.

Chứng minh tương tự ta có: Δ AHE, Δ AEC đều là các tam giác vuông tại A, E.

Xét tứ giác AHCE có Góc EAH = AHC = HCE = CEA = 90°

⇒ Tứ giác AHCE là hình chữ nhật. ( đ.p.c.m )

II. MỘT SỐ CÁCH CHỨNG MINH TỨ GIÁC LÀ HÌNH CHỮ NHẬT CỰC HAY

Cách 1: Chứng minh hình thang cân có một góc vuông là hình chữ nhật

Ví dụ: Cho hình thang cân ABCD với AB // CD, giả sử góc D = 90°. Chứng minh ABCD là hình chữ nhật

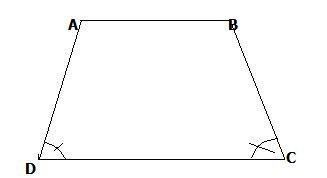
Theo giả thiết: Góc D = 90°

Ta có: AB // CD (ABCD là hình thang)

⇒ Góc A + D = 180° (hai góc trong cùng phía)
⇒ Góc A = 90°

Lại có Góc A + Góc C = 180° ⇒ Góc C = 90°

Vậy tứ giác ABCD có 3 góc A = B = C = 90°

⇒ ABCD là Hình chữ nhật. ( đ.p.c.m )

Cách 2: Chứng minh tứ giác có ba góc vuông là hình chữ nhật

Ví dụ: Cho tứ giác ABCD có ∆ABC vuông tại A, ∆BCD vuông tại B, ∆CDA vuông tại C. Tứ giác ABCD là hình gì. Vì sao?

Theo bài ra, ta có:

∆ABC vuông tại A ⇒ Góc BAC = 90°

∆BCD vuông tại B ⇒ Góc CBD = 90°

∆CDA vuông tại C ⇒ Góc DCA = 90°

⇒ Góc ADC = 90° (Tổng 4 góc của một tứ giác bừng 360 độ)

⇒ Tứ giác ABCD là hình chữ nhật do có bốn góc vuông. ( đ.p.c.m )

Cách 3: Chứng minh hình bình hành có hai đường chéo bằng nhau là hình chữ nhật

Ví dụ: Cho tam giác ABC cân tại A, các đường trung tuyến BM, CN cắt nhau tại G. Gọi D là điểm đối xứng với B qua M, gọi E là điểm đối xứng với G qua N. Tứ giác BEDC là hình gì? Vì sao?

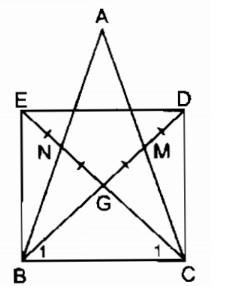
Theo bài ra, ta có: G là trọng tâm của ΔABC.

⇒ GB = 2GM và GC = 2GN

Điểm D đối xứng với điểm G qua điểm M
⇒ MG = MD hay GD = 2GM
Suy ra: GB = GD (3)

Điểm E đối xứng với điểm G qua điểm N
⇒ NG = NE hay GE = 2GN
Suy ra: GC = GE (4)

Từ (3) và (4) ⇒ Tứ giác BCDE là Hình bình hành do hai đường chéo cắt nhau tại trung điểm mỗi đường. (5)

Xét ΔBCM và ΔCNB, có:

BC cạnh chung
Góc BCM = CBN (tính chất tam giác cân)
CM = BN (vì AB = AC)

Suy ra: ΔBCM = ΔCBN (c.g.c)

⇒ Góc B₁ = C₁ ⇒ ΔGBC cân tại G ⇒ GB = GC ⇒ BD = CE (6)

Từ (5) và (6), suy ra: BCDE là hình chữ nhật do là hình bình hành có hai đường chéo bằng nhau. ( đ.p.c.m )

Cách 4: Chứng minh hình bình hành có một góc vuông là hình chữ nhật

Ví dụ: Cho tam giác ABC vuông cân tại C. Trên cạnh AC, BC lấy lần lượt các điểm P, Q sao cho AP = CQ. Từ điểm P vẽ PM // BC (M thuộc AB). Chứng minh tứ giác PCQM là hình chữ nhật.

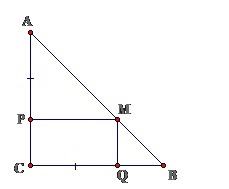
Theo bài ra, ta có:

∆ABC vuông tại C ⇒ AC ⊥ BC = > AP ⊥ PM

⇒ ∆APM vuông cân tại P

⇒ AP = PM

Lại có: AP = CQ

Mà PM // CQ

⇒ MNPQ là hình bình hành (1)

Mặt khác: Góc C = 90° (2)

Từ (1) và (2) ⇒ Tứ giác MNPQ là hình chữ nhật ( đ.p.c.m )

III. BÀI TẬP CHỨNG MINH TỨ GIÁC LÀ HÌNH CHỮ NHẬT

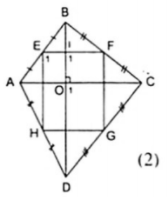
Bài 1: Cho hình bình hành ABCD. Các tia phân giác của các góc A, B, C, D cắt nhau như trên hình vẽ. Chứng minh rằng EFGH là hình chữ nhật.

Giải

 

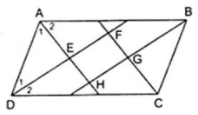
Đặt  

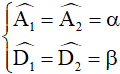
Áp dụng tính chất góc trong cùng phía vào AB//CD, ta được:

 

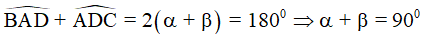
Áp dụng tính chất về góc vào ΔADE , ta được:  , hay

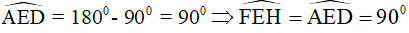  (đối đỉnh)

Chứng minh tương tự ta được  .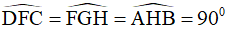

Tứ giác EFGH có bốn góc vuông nên nó là hình chữ nhật.

Bài 2: Tứ giác ABCD có hai đường chéo vuông góc với nhau. Gọi E, F, G, H lần lượt là trung điểm của các cạnh AB, BC, CD, DA. Tứ giác EFGH là hình gì? Vì sao?

Giải

Tứ giác EFGH là hình chữ nhật.

Giải thích: Từ giả thiết ta có EF, GH thứ tự là đường trung bình của các tam giác ABC và ADC. 

Áp dụng định lí đường trung bình vào hai tam giác này ta được:

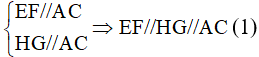
Chứng minh tương tự, ta cũng được EH//FG//BD.        (2)

 Từ (1) và (2) suy ra tứ giác EFGH có các cạnh đối song song nên nó là hình bình hành.

Gọi O là giao điểm của AC với BD và I là giao điểm của EF với BD

Áp dụng tính chất góc đồng vị vào các đường thẳng song song ở trên và giả thiết ta có:

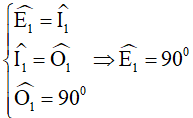
Như vậy hình bình hành EFGH có một góc vuông nên nó là hình chữ nhật.

Bài 3: Cho tứ giasc ABCD có AC ⊥ BD. Gọi E, F, G, H lần lượt là trung điểm của AB, BC, CD, DA. Chứng minh rằng tứ giác EFGH là hình chữ nhật.

Bài làm:

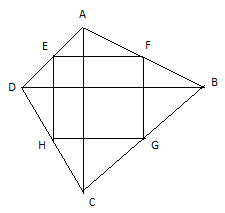
E, F là trung điểm của AB và BC nên EF là đường trung bình của ΔABC

⇒ EF // AC; EF = 12AC (1)

G, H là trung điểm của CD và DA nên GH là đường trung bình của ΔADC

⇒ GH // AC; GH = 12AC (2)

Từ (1) và (2) ⇒ EF // GH và EF = GH

⇒ tứ giác EFGH là hình bình hành.

Lại có E, H là trung điểm của AB và AD

⇒ EH là đường trung bình của ΔADB

⇒ EH // BD

Mà AC ⊥ BD; HG // AC

⇒ EH ⊥ GH

Hình bình hành EFGH có EH ⊥ GH do đó tứ giác EFGH là hình chữ nhật.

Bài 4 Cho ΔABC vuông tại A, AB < AC, đường cao AH. Lấy điểm E trên cạnh AC sao cho AE = AB. Gọi I là trung điểm của BE, kẻ EK ⊥ BC (K ∈ BC), EN ⊥ AH (N ∈ AH)

a) Chứng minh rằng tứ giác NEKH là hình chữ nhật.

b) IHAˆ=IHCˆ

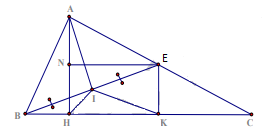
a) Tứ giác NEKH có 3 góc vuông nên là hình chữ nhật

b) Ta đi chứng minh ΔIHA = ΔIHK

Xét ΔABH và ΔAEN có:

• AB = AE
• BAHˆ=AENˆ (cùng phụ với ABHˆ)

⇒ ΔABH = ΔAEN

⇒ AH = NE. Mà NE = HK nên AH = HK

Xét ΔIHA và ΔIHK :

• IH chung
• AI = IK (= 12BE)
• AH = HK

⇒ ΔIHA = ΔIHK (c.c.c)

⇒IHAˆ=IHCˆ

Bài 5: Cho tam giác ABC, đường cao AH. Gọi I là trung điểm của AC. Lấy E là điểm đối xứng với H qua I. Gọi M, N lần lượt là trung điểm của HC, CE. Các đường thẳng AM, AN cắt HE tại G và K.

a. Chứng minh tứ giác AHCE là hình chữ nhật

b. Chứng minh HG = GK = KE

Hướng dẫn:

a. Chứng minh tứ giác AHCE là hình bình hành, có AHC=90⁰

⇒⋄AHCE là hình chữ nhật

b. Chứng minh G, K lần lượt là các trọng tâm của tam giác AHC, AEC và sử dụng tính chất 2 đường chéo của HCN

Bài 6: Cho tam giác ABC, các đường cao AD, BE, CF cắt nhau tại H, gọi I, K, R theo thứ tự là trung điểm của HA, HB, HC. Gọi M, N, P theo thứ tự là trung điểm của BC, AC, AB. Chứng minh rằng:

a. Tứ giác MNIK, PNRK là các hình chữ nhật

b. P, N, R, K, M, I cùng thuộc 1 đường tròn

c. D, E, F cũng thuộc đường tròn trên

Lời giải:

Ta có: OD=1/2IM

OE=1/2KN

OF=1/2PR    

Bài 7: Cho tam giác ABC vuông tại A, M thuộc BC. Gọi D và E là chân đường vuông góc kẻ từ M đến AB và AC

a. Định dạng tứ giác ADME

b. Gọi I là trung điểm của DE. Chứng minh A, I, M thẳng hàng

c. Điểm M nằm ở đâu trên BC thì DE nhỏ nhất. Tính DE trong trường hợp đó biết AB = 15cm, AC =20cm

Lời giải

a. Tứ giác ADME có 3 góc vuông nên là hình chữ nhật

c. DE nhỏ nhất khi AM nhỏ nhất ( DE = AM ). AM nhỏ nhất khi và chỉ khi AM = AH khi M trùng H Xét ΔABC vuông tại A

Suy ra BC = 25cm(pitago). Vậy S_ABC =1/2AH.BC
AH = AH.BC/BC= 12.20/25 = 12cm.

Trên đây, Mầm Non Ánh Dương đẫ giới thiệu đến quý bạn đọc lý thuyết hình chữ nhật. Cách chứng minh tứ giác là hình chữ nhật nhanh nhất. Hi vong, chia sẻ cùng bài viết bạn đã nắm chắc hơn chuyên đề hình chữ nhật, một chuyên đề hình học 8 vô cùng quan trọng. Xem thêm cách chứng minh tứ giác là hình bình hành tại đường link này bạn nhé !

Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục