Lí thuyết bất phương trình bậc nhất một ẩn và cách giải hay
Lí thuyết bất phương trình bậc nhất một ẩn học sinh đã được tìm hiểu trong chương trình Toán 8, phân môn Đại số. Nhằm giúp các em hệ thống lại tất cả các kiến thức cần ghi nhớ và cách giải bất phương trình hay, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các em tìm hiểu nhé !
I. LÝ THUYẾT VỀ BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
This post: Lí thuyết bất phương trình bậc nhất một ẩn và cách giải hay
1. Bất phương trình là gì?
Bất phương trình thường được định nghĩa dựa trên khái niệm mệnh đề một biến (hay còn gọi là hàm mệnh đề).
Bất phương trình thường bao gồm những loại sau đây:
- Bất phương trình bậc nhất một ẩn
- Bất phương trình bậc hai một ẩn.
- Bất phương trình bậc nhất hai ẩn.
2.Bất phương trình một ẩn là gì?
– bất phương trình một ẩn là bất phương trình có dạng f(x) > g(x) ( hoặc f(x) < g(x); f(x) ≥ g(x); f(x) ≤ g(x)), trong đó f(x) và g(x) là hai biểu thức của biến x.
– Số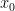 
gọi là nghiệm của phương trình f(x) > g(x) nếu thay 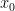vào ta được f(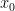) > g(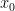) là một khẳng định đúng. Giải bất phương trình ta tìm được tất cả các nghiệm hay tập nghiệm của bất phương trình đó.
– Hai bất phương trình được gọi là tương đương nếu chùng có cùng tập nghiệm.
– Phép biến đổi một bất phương trình thành một bất phương trình tương đương gọi là phép biến đổi tương đương.
Một số quy tắc biến đổi tương đương thường dùng là :
- Chuyển vế : f(x) + h(x) > g(x) <=> f(x) > g(x) – h(x)
- Nhân (chia ) :
| f(x) > g(x) <=> f(x) .h(x) > g(x).h(x) nếu h(x) > 0 với mọi x
f(x) > g(x) <=> f(x) .h(x) < g(x).h(x) nếu h(x) < 0 với mọi x |
3. Bất phương trình bậc nhất một ẩn là gì?
– Bất phương trình một ẩn là bất phương trình có dạng ax + b > 0( hoặc ax + b < 0; ax + b ≥ 0; ax + b ≤ 0) trong đó a,b là các số cho trước và a ≠ 0.
– Giải bất phương trình ax + b > 0 (1)
Ta có (1) <=> ax > -b
+ Nếu a > 0 thì (1) <=> x > -b/a.
+ Nếu a < 0 thì (1) <=> x < -b/a.
+ Nếu a = 0 thì (1) trở thành 0x > -b
- Nếu b ≤ 0 thì (1) vô nghiệm
Nếu b > 0 thì (1) nghiệm đúng với mọi x R
4. Hai quy tắc biến đổi bất phương trình
a) Quy tắc chuyển vế
Khi chuyển một hạng tử của bất phương trình từ vế này sang vế kia ta đổi dấu hạng tử đó.
b) Quy tắc nhân với một số
Khi nhân hai vế của bất phương trình với cùng một số khác 0, ta phải:
– Giữ nguyên chiều bất phương trình nếu số đó dương.
– Đổi chiều bất phương trình nếu số đó âm.
5. Ví dụ
Áp dụng hai quy tắc biến đổi trên, ta giải bất phương trình bậc nhất một ẩn như sau:
Dạng: ax+b>0⇔ax>−b
⇔x>−b/a nếu a>0 hoặc x<−b/a nếu a<0
Vậy nghiệm của bất phương trình ax+b>0 là:
S1={x|x>−b/a,a>0} hoặc S2={x|x<−b/a,a<0}
II. CÁCH GIẢI BẤT PHƯƠNG TRÌNH BẬC NHẤT MỘT ẨN
Câu 1:
Giải chi tiết:
Nếu a > 0 thì ax + b > 0 ⇔ x > -b/a nên
S=x/x > -b/a #Ø
Nếu a < 0 thì ax + b > 0 ⇔ x < -b/a nên
S=x/x < -b/a #Ø
Nếu a = 0 thì ax + b > 0 có dạng 0x + b > 0
Ta có nếu b > 0 => S = R.
Ta có nếu b ≤ 0 => S = Ø
Chọn đáp án D.
Câu 2:
Giải chi tiết:
Ta có: 5x – 1 ≥ 2x/5+ 3 ⇔ 25x – 5 ≥ 2x + 15 ⇔ 23x ≥ 20 ⇔ x ≥ 20/23.
Vậy tập nghiệm S là x ≥ 20/23;
Chọn đáp án D.
Câu 3:
Giải chi tiết:
Ta có:
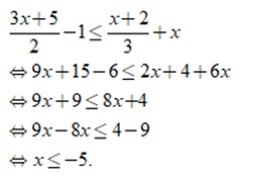
So sánh điều kiện => có 5 nghiệm nguyên.
Chọn đáp án B.
Câu 4:
Giải chi tiết:
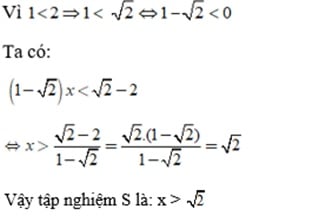
Vậy tập nghiệm S là: x > √2
Chọn đáp án B.
Câu 5:
Giải chi tiết:
Ta có: ( 2x – 1 )( x + 3 ) – 3x + 1 ≤ ( x – 1 )( x + 3 ) + x2 – 5
⇔ 2x2 + 5x – 3 – 3x + 1 ≤ x2 + 2x – 3 + x2 – 5 ⇔ 0x ≤ – 6
⇔ x thuộc tập hợp Ø vậy S = Ø
Chọn đáp án D.
Câu 6:
Giải chi tiết:
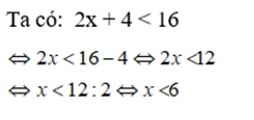
Chọn đáp án B
Câu 7:
Giải chi tiết:
Ta có: 8x + 4 > 2( x +5 )
⇔ 8x + 4 > 2x + 10
⇔ 6x > 6
⇔ x > 6 : 6
⇔ x > 1
Chọn đáp án D
Câu 8:
Giải chi tiết:
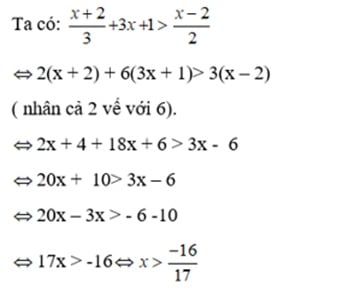
Chọn đáp án C
Câu 9:
Giải chi tiết:
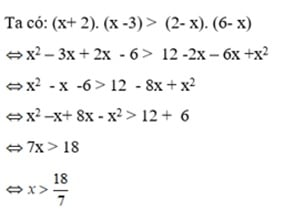
Chọn đáp án A
Câu 10:
Giải chi tiết:
X=2 :
⇔ 2m + 2 < 2 + 3 + m
⇔ 2m – m < 2 + 3- 2
⇔ m < 3
Chọn đáp án B
Câu 11:
Giải chi tiết:
– Bất phương trình a là bất phương trình bậc nhất một ẩn.
– Bất phương trình c là bất phương trình bậc nhất một ẩn.
– Bất phương trình b có chỉ số a = 0 không thỏa điều kiện là a ≠ 0 nên không phải là bất phương trình bậc nhất một ẩn.
– Bất phương trình d có mũ x là bậc 2 nên không phải là bất phương trình bậc nhất một ẩn.
Câu 12:
Giải chi tiết:
Sử dụng quy tắc chuyển vế và đổi dấu
- a) x – 5 > 3
⇔ x > 3 + 5
⇔ x > 8.
Vậy nghiệm của S là x > 8.
- b) x – 2x < -2x + 4
⇔ x – 2x + 2x < 4
⇔ x < 4
Vậy nghiệm của S là x < 4.
- c) -3x > -4x + 2
⇔ -3x + 4x > 2
⇔ x > 2
Vậy nghiệm của S là x > 2.
- d) 8x + 2 < 7x – 1
⇔ 8x – 7x < -1 – 2
⇔ x < -3
Vậy nghiệm của S là x < -3.
Vậy là các bạn vừa được tìm hiểu Lí thuyết bất phương trình bậc nhất một ẩn và cách giải hay. Hi vọng, sau khi chia sẻ cùng bài viết, bạn nắm vững hơn chuyên đề bất phương trình này. Chia sẻ thêm cách giải bài toán bằng cách lập phương trình nhé !
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục
