Hình cầu là gì? Công thức tính diện tích hình cầu, thể tích khối cầu Đầy Đủ

Ở bài viết trước, Mầm Non Ánh Dương đã giới thiệu đến quý thầy cô và các bạn học sinh công thức tính thể tích khối cầu. Tiếp nối mạch kiến thức đó, hôm nay chúng tôi sẽ giới thiệu về Công thức tính diện tích hình cầu và nhiều dạng bài tập thường gặp. Bạn chia sẻ để có thêm nhiều nguồn tư liệu bổ ích nhé !

I. LÝ THUYẾT VỀ HÌNH CẦU

This post: Hình cầu là gì? Công thức tính diện tích hình cầu, thể tích khối cầu Đầy Đủ

1. Hình cầu là gì?

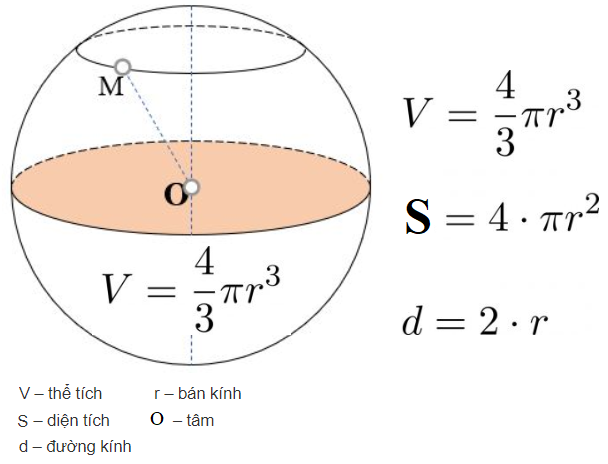
Trong không gian ba chiều, khi bạn xoay nửa hình tròn có tâm O, bán kính R một vòng quanh trục hay còn gọi là đường kính AB thì sẽ tạo thành một hình cầu.

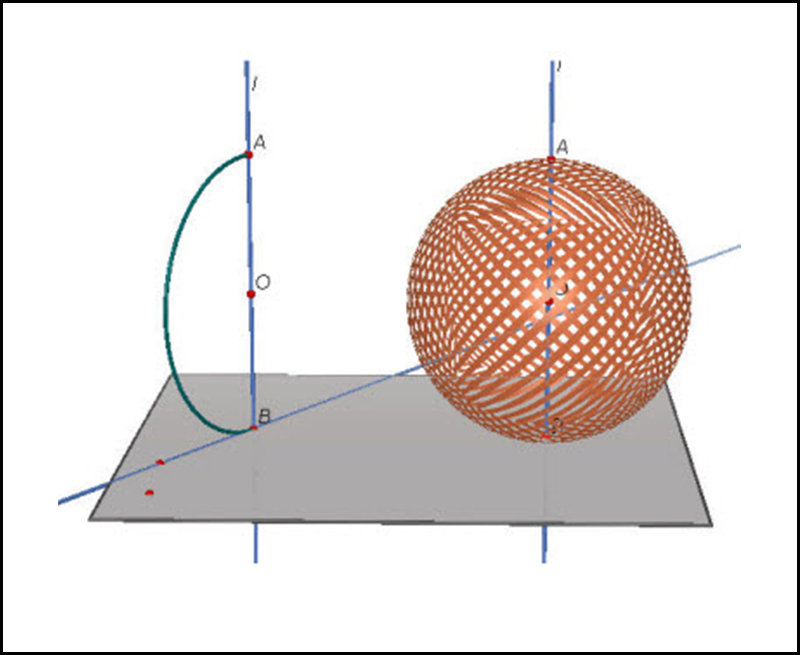
lxt9khssiit2n6zp6ihgum2hb2kbbyuchrjlzrnf-2

2. Mặt cầu là gì ?

Trong không gian ba chiều, mặt cầu là quỹ tích tập hợp các điểm cách đều một điểm O cố định cho trước một khoảng không đổi R.

Trong đó, O là tâm của hình cầu và khoảng cách R là bán kính.

3. Tính chất của hình cầu

Bất kỳ đường thẳng nào giao nhau với hình cầu và đi qua tâm của nó là trục đối xứng của hình. Xoay một quả cầu xung quanh trục này ở bất kỳ góc độ nào sẽ biến nó thành chính nó.
Một mặt phẳng cắt hình đang nghi vấn thông qua tâm của nó chia hình cầu thành hai phần bằng nhau, nghĩa là mặt phẳng phản xạ.

II. CÔNG THỨC TÍNH DIỆN TÍCH HÌNH CẦU

Tính diện tích mặt cầu giúp bạn tính được diện tích mặt cầu bên trong hình cầu.

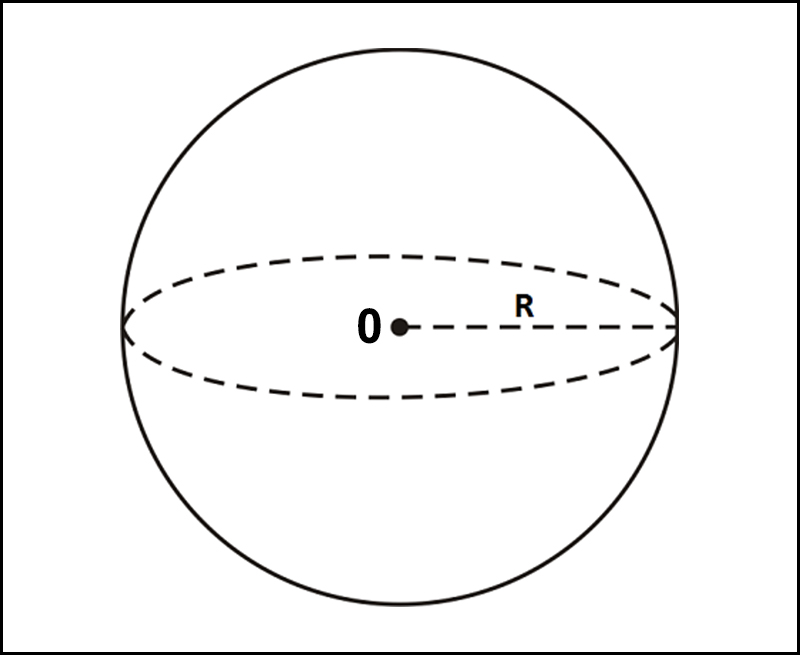
S = 4 * pi * R ², trong đó R là bán kính hình cầu, pi 3.14

Công thức chứng minh rằng diện tích S có thể được tính với điều kiện bán kính của hình được biết. Nếu đường kính D của nó được biết đến, thì công thức hình cầu có thể được viết là:

S = pi * D ², trong đó pi 3.14, d là đường kính hình cầu

Số pi không hợp lý, trong đó bốn vị trí thập phân được đưa ra, có thể được sử dụng trong một số phép tính toán học với độ chính xác hàng trăm, đó là 3, 14.

Cũng rất thú vị khi xem xét câu hỏi có bao nhiêu người vô trùng tương ứng với toàn bộ bề mặt của hình vẽ trong câu hỏi. Dựa trên định nghĩa của giá trị này, chúng tôi có được:

S / R ² = 4 * pi * R ² / R ² = 4 * pi steradian

Để tính bất kỳ góc thể tích nào, hãy thay thế giá trị tương ứng của khu vực S trong biểu thức trên.

Ví dụ:

Mình sẽ hướng dẫn bạn cách tính diện tích mặt cầu thông qua ví dụ như sau: Cho một hình cầu có bán kính từ tâm O dài 6cm. Hỏi diện tích của mặt cầu là bao nhiêu?

Áp dụng công thức trên, bạn có thể tính được diện tích mặt cầu như sau:

S = 4.π.r² = 4.π.6² = 114.π cm²

III. CÔNG THỨC TÍNH THỂ TÍCH KHỐI CẦU (HÌNH CẦU)

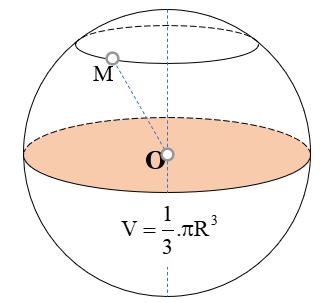
Trong đó:

V là thể tích khối cầu (đơn vị m³)
π là số pi, có giá trị sấp sỉ 3,14
r là bán kính khối cầu
d là bánh kính mặt cầu/hình cầu

Tổng hợp tất cả các công thức cần ghi nhớ về hình cầu, khối cầu:

o5pl8g09cbqigozjl7jxhy1w9mltkrjs1cc1f9rp-1

III. BÀI TẬP VỀ DIỆN TÍCH HÌNH CẦU VÀ THỂ TÍCH KHỐI CẦU

Bài 1: Với các bán kính nối từ tâm O dưới đây, bạn tính diện tích mặt cầu:

a. 9m

b. 1,5dm

c. 2cm

d. 15cm

Giải: Bạn đã biết bán kinh của mặt cầu. Soi vào công thức Smặt cầu = 4 π.R^2, bạn đã có đủ yếu tố để tính diện tích của mặt cầu này bằng cách thay số vào công thức trên, ta được:

a. S = 4 x 3,14 x 9^2 = 1017.36 m2

b. S = 4 x 3,14 x 1,5^2 = 28.26 dm2

c. S = 4 x 3,14 x 2^2 = 50.24 cm2

d. S = 4 x 3,14 x 15^2 = 2826 cm2

Bài 2: Với đường kính có độ dài cho như dưới đây, tính diện tích mặt cầu:

a. 2,5cm

b. 10cm

c. 1/2cm

d. 4,5cm

Giải: Đề bài đã cho độ dài đường kính cụ thể, do đó ta hoàn toàn có thể tính diện tích mặt cầu theo công thức: Smặt cầu = π. d2

a. S = 3,14 x 2,5^2 = 19,625 cm2

b. S = 3,14 x 10^2 = 314 cm2

c. S = 3,14 x 1/4 = 0,785 cm2

d. S = 3,14 x 4,5^2 = 63,585 cm2

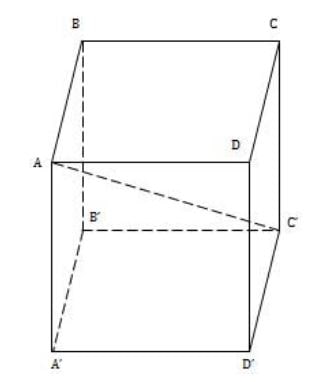
Bài 3: Đề bài yêu cầu tính thể tích khối cầu của hình lập phương ABCD.A’B’C’D’ có độ dài các cạnh là a. Tính thể tích khối cầu như sau:

a. Tính thể tích khối cầu ngoại tiếp hình lập phương

b, Tính thể tích khối cầu nội tiếp hình lập phương

Giải:

tính thể tích hình cầu

Tính thể tích khối cầu hình lập phương.

Bài 4: Cho hình tròn có chu vi là 31,4 cm. Hãy tính thể tích hình cầu có bán kính bằng bán kính của hình tròn vừa cho.

Giải:

Chu vi hình tròn C = 2πr = 31.4 cm

=> Bán kính r = C/2π = 5 cm

Thể tích khối cầu đã cho là:

V = ⁴⁄₃πr³ = 4/3.3,14.(5)³ = 523,3 cm³

Bài 5: Cho tứ diện đều ABCD có cạnh đáy bằng a. Thể tích khối cầu ngoại tiếp tứ diện ABCD bằng:

$A. frac{pi {{a}^{3}}sqrt{6}}{8}$	$B. frac{pi {{a}^{3}}sqrt{6}}{6}$
$C. frac{pi {{a}^{3}}sqrt{6}}{4}$	$D.frac{3pi {{a}^{3}}sqrt{6}}{8}$

Bài 6: Tính thể tích khối cầu có đường kính d = 4 cm.

Giải:

Bán kính r = d/2 = 2 cm

Thể tích khối cầu là:

V = ⁴⁄₃πr³ = 4/3.3,14.(2)³ = 33,49 cm³

Bài 7: Gọi (S) là mặt cầu có tâm O và bán kính r, d là khoảng cách từ O đến mặt phẳng (P), d < r. Khi đó có bao nhiêu điểm chung giữa (S), (P)?

A. Vô số	B. 1
C. 0	D. 2

Bài 8: Cho mặt cầu có diện tích bằng $frac{8pi {{a}^{2}}}{3}$ . Khi đó, bán kính mặt cầu là:

$A. frac{asqrt{3}}{3}$	$B. frac{asqrt{6}}{3}$
$C.frac{asqrt{6}}{2}$	$D. frac{asqrt{2}}{3}$

Bài 9:

Nếu thể tích của một hình cầu là 1131711317 thì trong các kết quả sau đây, kết quả nào là bán kính của nó (lấy π=227π=227)?

A. 2 cm

B. 3 cm

C. 5 cm

D. 6 cm

E. Một kết quả khác.

Bài 10:

Cho nửa đường tròn tâm O, đường kính AB = 2R, Ax và By là hai tiếp tuyến với nửa đường tròn tại A và B. Lấy trên tia Ax điểm M rồi vẽ tiếp tuyến MP cắt By tại N.

a. Chứng minh rằng MON và APB là hai tam giác vuông đồng dạng.

b. Chứng minh rằng AM.BN=R2AM.BN=R2

c. Tính tỉ số SMONSAPBSMONSAPB khi AMAM = R2.R2.

d. Tính thể tích của hình do nửa hình tròn APB quay quanh AB sinh ra.

Trên đây là toàn bộ kiến thức về công thức tính diện tích hình cầu, thể tích khối cầu đầy đủ và nhiều dạng bài tập thường gặp. Hãy nhanh tay lưu lại để xem khi cần bạn nhé ! Chúc các bạn luôn dạy tốt, học tốt ! Hẹn gặp lại các bạn trong những bài viết sau !

Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục