Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay
Định lý Thales (hay Định lý Talet) là một định lý rất quan trọng trong hình học không gian của nhà toán học người Hy Lạp Thales. Bài viết hôm nay, Mầm Non Ánh Dương sẽ tổng hợp lại tất cả các kiến thức liên quan về định lí này cũng như cách áp dụng định lí Thales vào giải toán cực hay. Bạn tìm hiểu nhé !
I. ĐỊNH LÍ THALES TRONG TAM GIÁC
This post: Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay
Định lý Thalès được phát biểu như sau: Nếu 1 đường thẳng song song với 1 cạnh của tam giác đó và cắt 2 cạnh còn lại thì nó định ra trên 2 cạnh đó những đoạn thẳng tương ứng tỉ lệ.
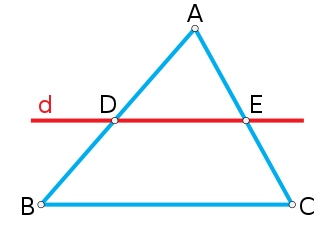
Tại hình vẽ bên nếu có: tam giác ABC – d cắt AB tại D, cắt AC tại E, song song với BC, như vậy theo định lý Thalès, ta có được:
và
và
.
1. Định lý Talet đảo trong tam giác
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Cho tam giác ABC nếu:
AB′AB=AC′AC
AB′BB′=AC′CC′
BB′AB=CC′AC
=> a//BC
2. Hệ quả của định lí Talet
Nếu một đường thẳng cắt hai cạnh (hoặc cắt phần kéo dài của hai cạnh) của một tam giác và cũng song song với cạnh còn lại thì nó sẽ tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.
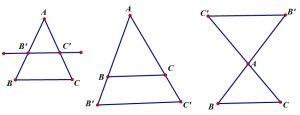
=> AB′AB=AC′AC=B′C′BC
II. ĐỊNH LÍ THALES TRONG HÌNH THANG
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.
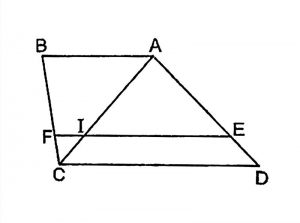
Cho hình thang ABCD, điểm E thuộc AD và F thuộc BC
Nếu EF // AB // CD, ta có AEDE=BFCF
Ngược lại, nếu: AEDE=BFCF => EF // AB// CD
Ví dụ : Cho hình thang ABCD (AB // CD) AB < CD. Đường thẳng MN // với 2 đáy cắt cạnh AD, BC lần lượt tại M và N. Biết AD = 2cm, AM = 3cm, BC = 6cm. Tìm độ dài BN.
Giải: Vì hình thang ABCD có AB // CD // MN
Theo định lý Talet trong hình thang ABCD ta có, ⇒AMAD=BNBC⇒BN=AM.BCAD=3.62=9
III. ĐỊNH LÍ THALES TRONG KHÔNG GIAN
Ba mặt phẳng song song chắn trên 2 đường thẳng những đoạn thẳng tỉ lệ
Định lý đảo
Cho 2 đường thẳng và
chéo nhau. Lấy các điểm
,
,
và
,
,
sao cho
Khi đó các đường thẳng
,
,
cùng song song với một mặt phẳng.
IV. BÀI TẬP ÁP DỤNG ĐỊNH LÍ THALES
Bài 1: Cho góc xOy. Trên tia Ox, lấy theo thứ tự 2 điểm A, B sao cho OA = 2cm, AB = 3cm. Trên tia Oy, lấy điểm C với OC = 3cm. Từ B, kẻ đường thẳng song song với AC cắt OY tại D. Tính độ dài CD.
Bài 2: Cho ∆ABC với trọng tâm G của tam giác. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh:
Bài 3: Cho ∆ABC có AB = 7,5cm. Trên AB lấy điểm D với.
a) Tính DA, DB
b) Kẻ DHAC tại H, BKAC tại K. Tính tỉ số DH v BK.
c) Cho biết AK = 4,5cm. Tính HK.
Bài 4: Cho ∆ABC. Từ điểm D trện cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AB và AC theo thứ tự E và F. Tính:
Bài 5: Cho ∆ABC. Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF = DB. Gọi M là giao điểm DF và BC. Chứng minh
Bài 6: Cho hình bình hnh ABCD, MBC, điểm N thuộc tia đối của tia BC sao cho BN = CM. Các đường thẳng DN, DM cắt AB theo thứ tự tại E, F.
Chứng minh rằng: AE2 = EB.EF
Bài 7: Một đường thẳng đi qua đỉnh A của hình bình hnh ABCD cắt BD, BC, DC theo thứ tự ở E, K,G. Chứng minh rằng:
AE2= EK.EG
Bài 8: Cho ∆ABC có BC = 10cm. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N. Tính DM và EN.
Bài 9: Hình thang ABCD (AB//CD, AB<CD) cĩ hai đường chéo AC và BD cắt nhau tại O. Chứng minh rằng: OA.OD = OB.OC
Bài 10: Cho hình thang ABCD (AB//CD, AB<CD). Đường thẳng song song với đáy AB cắt các cạnh bên và đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. Chứng minh rằng: MN = PQ.
Bài 11: Cho hình thang ABCD (AB//CD, AB<CD). Gọi trung điểm của các đường chéo AC và BD theo thứ tự là N và M. Chứng minh rằng:
a) MN // AB
b) MN=CD-AB/2
Bài 12: Hình thang ABCD (AB//CD,AB<CD) cĩ 2 đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD và BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
Bài 13: Cho hình thang ABCD (AB//CD,AB<CD). Gọi M l trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM v AC.
a) Chứng minh: IK // AB.
b) Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh: EI = IK = KF.
Bài 14: Cho ∆ABC vuông tại A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE vuơng gĩc DC (E thuộc AC); DK vuơng gĩc AC (K thuộc AC). Chứng minh: BE // HK
Bài 15: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Vẽ IM // BK (M thuộc AC), vẽ KN // CI (N thuộc AB). Chứng minh: MN // BC.
Bài viết trên đây, chúng tôi đã giới thiệu đến quý thầy cô và các bạn Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay. Hi vọng, đây sẽ là nguồn tư liệu hữu ích giúp bạn dạy và học tốt hơn. Chia sẻ thêm định lí Pytago và cách ứng dụng định lí Pytago nữa bạn nhé !
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay
Định lý Thales (hay Định lý Talet) là một định lý rất quan trọng trong hình học không gian của nhà toán học người Hy Lạp Thales. Bài viết hôm nay, Mầm Non Ánh Dương sẽ tổng hợp lại tất cả các kiến thức liên quan về định lí này cũng như cách áp dụng định lí Thales vào giải toán cực hay. Bạn tìm hiểu nhé !
I. ĐỊNH LÍ THALES TRONG TAM GIÁC
This post: Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay
Định lý Thalès được phát biểu như sau: Nếu 1 đường thẳng song song với 1 cạnh của tam giác đó và cắt 2 cạnh còn lại thì nó định ra trên 2 cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Tại hình vẽ bên nếu có: tam giác ABC – d cắt AB tại D, cắt AC tại E, song song với BC, như vậy theo định lý Thalès, ta có được:
và
và
.
1. Định lý Talet đảo trong tam giác
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Cho tam giác ABC nếu:
AB′AB=AC′AC
AB′BB′=AC′CC′
BB′AB=CC′AC
=> a//BC
2. Hệ quả của định lí Talet
Nếu một đường thẳng cắt hai cạnh (hoặc cắt phần kéo dài của hai cạnh) của một tam giác và cũng song song với cạnh còn lại thì nó sẽ tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

=> AB′AB=AC′AC=B′C′BC
II. ĐỊNH LÍ THALES TRONG HÌNH THANG
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.

Cho hình thang ABCD, điểm E thuộc AD và F thuộc BC
Nếu EF // AB // CD, ta có AEDE=BFCF
Ngược lại, nếu: AEDE=BFCF => EF // AB// CD
Ví dụ : Cho hình thang ABCD (AB // CD) AB < CD. Đường thẳng MN // với 2 đáy cắt cạnh AD, BC lần lượt tại M và N. Biết AD = 2cm, AM = 3cm, BC = 6cm. Tìm độ dài BN.
Giải: Vì hình thang ABCD có AB // CD // MN
Theo định lý Talet trong hình thang ABCD ta có, ⇒AMAD=BNBC⇒BN=AM.BCAD=3.62=9
III. ĐỊNH LÍ THALES TRONG KHÔNG GIAN
Ba mặt phẳng song song chắn trên 2 đường thẳng những đoạn thẳng tỉ lệ
Định lý đảo
Cho 2 đường thẳng và
chéo nhau. Lấy các điểm
,
,
và
,
,
sao cho
Khi đó các đường thẳng
,
,
cùng song song với một mặt phẳng.
IV. BÀI TẬP ÁP DỤNG ĐỊNH LÍ THALES
Bài 1: Cho góc xOy. Trên tia Ox, lấy theo thứ tự 2 điểm A, B sao cho OA = 2cm, AB = 3cm. Trên tia Oy, lấy điểm C với OC = 3cm. Từ B, kẻ đường thẳng song song với AC cắt OY tại D. Tính độ dài CD.
Bài 2: Cho ∆ABC với trọng tâm G của tam giác. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh:
Bài 3: Cho ∆ABC có AB = 7,5cm. Trên AB lấy điểm D với.
a) Tính DA, DB
b) Kẻ DHAC tại H, BKAC tại K. Tính tỉ số DH v BK.
c) Cho biết AK = 4,5cm. Tính HK.
Bài 4: Cho ∆ABC. Từ điểm D trện cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AB và AC theo thứ tự E và F. Tính:
Bài 5: Cho ∆ABC. Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF = DB. Gọi M là giao điểm DF và BC. Chứng minh
Bài 6: Cho hình bình hnh ABCD, MBC, điểm N thuộc tia đối của tia BC sao cho BN = CM. Các đường thẳng DN, DM cắt AB theo thứ tự tại E, F.
Chứng minh rằng: AE2 = EB.EF
Bài 7: Một đường thẳng đi qua đỉnh A của hình bình hnh ABCD cắt BD, BC, DC theo thứ tự ở E, K,G. Chứng minh rằng:
AE2= EK.EG
Bài 8: Cho ∆ABC có BC = 10cm. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N. Tính DM và EN.
Bài 9: Hình thang ABCD (AB//CD, AB<CD) cĩ hai đường chéo AC và BD cắt nhau tại O. Chứng minh rằng: OA.OD = OB.OC
Bài 10: Cho hình thang ABCD (AB//CD, AB<CD). Đường thẳng song song với đáy AB cắt các cạnh bên và đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. Chứng minh rằng: MN = PQ.
Bài 11: Cho hình thang ABCD (AB//CD, AB<CD). Gọi trung điểm của các đường chéo AC và BD theo thứ tự là N và M. Chứng minh rằng:
a) MN // AB
b) MN=CD-AB/2
Bài 12: Hình thang ABCD (AB//CD,AB<CD) cĩ 2 đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD và BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
Bài 13: Cho hình thang ABCD (AB//CD,AB<CD). Gọi M l trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM v AC.
a) Chứng minh: IK // AB.
b) Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh: EI = IK = KF.
Bài 14: Cho ∆ABC vuông tại A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE vuơng gĩc DC (E thuộc AC); DK vuơng gĩc AC (K thuộc AC). Chứng minh: BE // HK
Bài 15: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Vẽ IM // BK (M thuộc AC), vẽ KN // CI (N thuộc AB). Chứng minh: MN // BC.
Bài viết trên đây, chúng tôi đã giới thiệu đến quý thầy cô và các bạn Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay. Hi vọng, đây sẽ là nguồn tư liệu hữu ích giúp bạn dạy và học tốt hơn. Chia sẻ thêm định lí Pytago và cách ứng dụng định lí Pytago nữa bạn nhé !
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay
Định lý Thales (hay Định lý Talet) là một định lý rất quan trọng trong hình học không gian của nhà toán học người Hy Lạp Thales. Bài viết hôm nay, Mầm Non Ánh Dương sẽ tổng hợp lại tất cả các kiến thức liên quan về định lí này cũng như cách áp dụng định lí Thales vào giải toán cực hay. Bạn tìm hiểu nhé !
I. ĐỊNH LÍ THALES TRONG TAM GIÁC
This post: Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay
Định lý Thalès được phát biểu như sau: Nếu 1 đường thẳng song song với 1 cạnh của tam giác đó và cắt 2 cạnh còn lại thì nó định ra trên 2 cạnh đó những đoạn thẳng tương ứng tỉ lệ.

Tại hình vẽ bên nếu có: tam giác ABC – d cắt AB tại D, cắt AC tại E, song song với BC, như vậy theo định lý Thalès, ta có được:
và
và
.
1. Định lý Talet đảo trong tam giác
Nếu một đường thẳng cắt hai cạnh của một tam giác và định ra trên hai cạnh này những đoạn thẳng tương ứng tỉ lệ thì đường thẳng đó song song với cạnh còn lại của tam giác.
Cho tam giác ABC nếu:
AB′AB=AC′AC
AB′BB′=AC′CC′
BB′AB=CC′AC
=> a//BC
2. Hệ quả của định lí Talet
Nếu một đường thẳng cắt hai cạnh (hoặc cắt phần kéo dài của hai cạnh) của một tam giác và cũng song song với cạnh còn lại thì nó sẽ tạo thành một tam giác mới có ba cạnh tương ứng tỉ lệ với ba cạnh của tam giác đã cho.

=> AB′AB=AC′AC=B′C′BC
II. ĐỊNH LÍ THALES TRONG HÌNH THANG
Nếu một đường thẳng song song với hai đáy của hình thang và cắt hai cạnh bên thì nó định ra trên hai cạnh bên đó những đoạn thẳng tương ứng tỉ lệ.

Cho hình thang ABCD, điểm E thuộc AD và F thuộc BC
Nếu EF // AB // CD, ta có AEDE=BFCF
Ngược lại, nếu: AEDE=BFCF => EF // AB// CD
Ví dụ : Cho hình thang ABCD (AB // CD) AB < CD. Đường thẳng MN // với 2 đáy cắt cạnh AD, BC lần lượt tại M và N. Biết AD = 2cm, AM = 3cm, BC = 6cm. Tìm độ dài BN.
Giải: Vì hình thang ABCD có AB // CD // MN
Theo định lý Talet trong hình thang ABCD ta có, ⇒AMAD=BNBC⇒BN=AM.BCAD=3.62=9
III. ĐỊNH LÍ THALES TRONG KHÔNG GIAN
Ba mặt phẳng song song chắn trên 2 đường thẳng những đoạn thẳng tỉ lệ
Định lý đảo
Cho 2 đường thẳng và
chéo nhau. Lấy các điểm
,
,
và
,
,
sao cho
Khi đó các đường thẳng
,
,
cùng song song với một mặt phẳng.
IV. BÀI TẬP ÁP DỤNG ĐỊNH LÍ THALES
Bài 1: Cho góc xOy. Trên tia Ox, lấy theo thứ tự 2 điểm A, B sao cho OA = 2cm, AB = 3cm. Trên tia Oy, lấy điểm C với OC = 3cm. Từ B, kẻ đường thẳng song song với AC cắt OY tại D. Tính độ dài CD.
Bài 2: Cho ∆ABC với trọng tâm G của tam giác. Qua G vẽ đường thẳng song song với AB cắt BC tại D. Chứng minh:
Bài 3: Cho ∆ABC có AB = 7,5cm. Trên AB lấy điểm D với.
a) Tính DA, DB
b) Kẻ DHAC tại H, BKAC tại K. Tính tỉ số DH v BK.
c) Cho biết AK = 4,5cm. Tính HK.
Bài 4: Cho ∆ABC. Từ điểm D trện cạnh BC, kẻ các đường thẳng song song với các cạnh AB và AC, chúng cắt các cạnh AB và AC theo thứ tự E và F. Tính:
Bài 5: Cho ∆ABC. Từ D trên cạnh AB, kẻ đường thẳng song song với BC cắt AC tại E. Trên tia đối của tia CA, lấy điểm F sao cho CF = DB. Gọi M là giao điểm DF và BC. Chứng minh
Bài 6: Cho hình bình hnh ABCD, MBC, điểm N thuộc tia đối của tia BC sao cho BN = CM. Các đường thẳng DN, DM cắt AB theo thứ tự tại E, F.
Chứng minh rằng: AE2 = EB.EF
Bài 7: Một đường thẳng đi qua đỉnh A của hình bình hnh ABCD cắt BD, BC, DC theo thứ tự ở E, K,G. Chứng minh rằng:
AE2= EK.EG
Bài 8: Cho ∆ABC có BC = 10cm. Trên cạnh AB lấy các điểm D và E sao cho AD = DE = EB. Từ D, E kẻ các đường thẳng song song với BC, cắt cạnh AC theo thứ tự tại M, N. Tính DM và EN.
Bài 9: Hình thang ABCD (AB//CD, AB<CD) cĩ hai đường chéo AC và BD cắt nhau tại O. Chứng minh rằng: OA.OD = OB.OC
Bài 10: Cho hình thang ABCD (AB//CD, AB<CD). Đường thẳng song song với đáy AB cắt các cạnh bên và đường chéo AD, BD, AC và BC theo thứ tự tại các điểm M, N, P, Q. Chứng minh rằng: MN = PQ.
Bài 11: Cho hình thang ABCD (AB//CD, AB<CD). Gọi trung điểm của các đường chéo AC và BD theo thứ tự là N và M. Chứng minh rằng:
a) MN // AB
b) MN=CD-AB/2
Bài 12: Hình thang ABCD (AB//CD,AB<CD) cĩ 2 đường chéo AC và BD cắt nhau tại O. Đường thẳng qua O và song song với đáy AB cắt các cạnh bên AD và BC theo thứ tự tại M, N. Chứng minh rằng OM = ON.
Bài 13: Cho hình thang ABCD (AB//CD,AB<CD). Gọi M l trung điểm của CD. Gọi I là giao điểm của AM và BD, K là giao điểm của BM v AC.
a) Chứng minh: IK // AB.
b) Đường thẳng IK cắt AD, BC theo thứ tự ở E và F. Chứng minh: EI = IK = KF.
Bài 14: Cho ∆ABC vuông tại A, đường cao AH. Từ điểm D nằm giữa H và C, vẽ DE vuơng gĩc DC (E thuộc AC); DK vuơng gĩc AC (K thuộc AC). Chứng minh: BE // HK
Bài 15: Cho tam giác ABC, điểm I thuộc cạnh AB, điểm K thuộc cạnh AC. Vẽ IM // BK (M thuộc AC), vẽ KN // CI (N thuộc AB). Chứng minh: MN // BC.
Bài viết trên đây, chúng tôi đã giới thiệu đến quý thầy cô và các bạn Định lí Thales và cách ứng dụng định lí Thales vào giải toán cực hay. Hi vọng, đây sẽ là nguồn tư liệu hữu ích giúp bạn dạy và học tốt hơn. Chia sẻ thêm định lí Pytago và cách ứng dụng định lí Pytago nữa bạn nhé !
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục




