Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

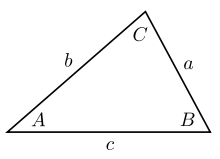
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

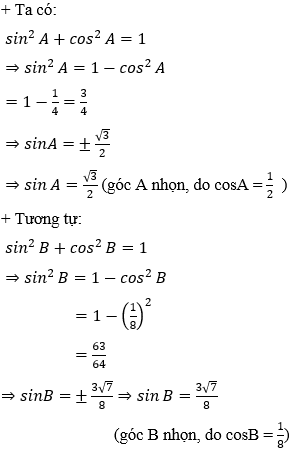
Ví dụ 2: Cho tam giác 

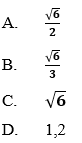
Hướng dẫn giải:

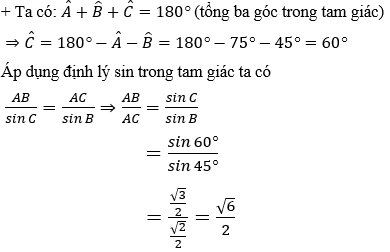
Đáp án A

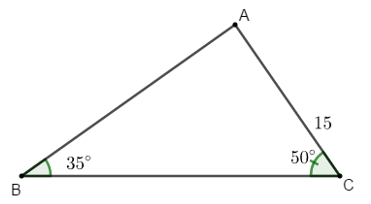
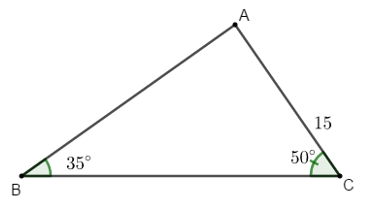
Ví dụ 3: Cho tam giác ABC có 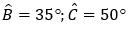 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

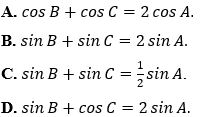
Hướng dẫn giải:

Đáp án B

Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

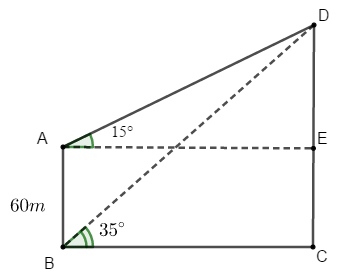
Áp dụng định lý sin trong tam giác ABD ta có:

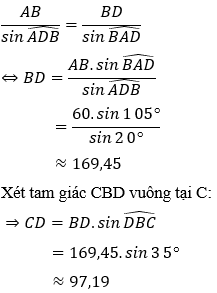
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

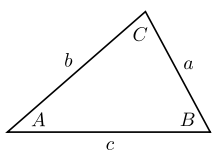
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

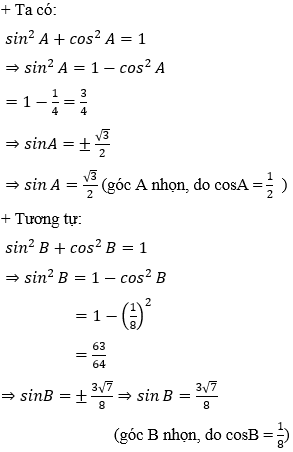
Ví dụ 2: Cho tam giác 

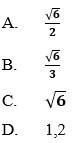
Hướng dẫn giải:

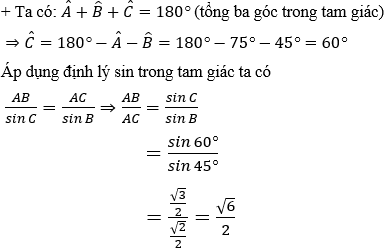
Đáp án A

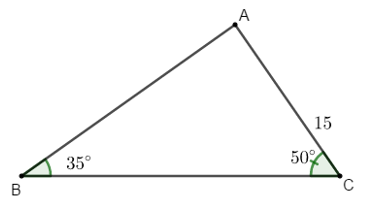
Ví dụ 3: Cho tam giác ABC có 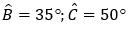 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

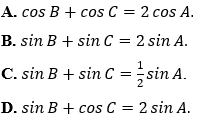
Hướng dẫn giải:

Đáp án B

Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

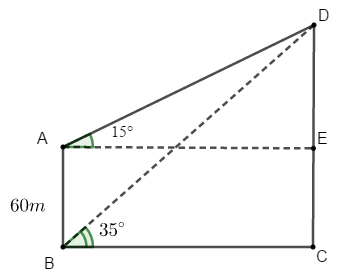
Áp dụng định lý sin trong tam giác ABD ta có:

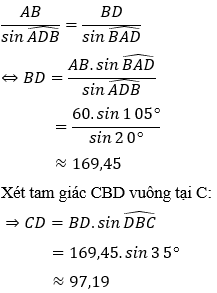
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

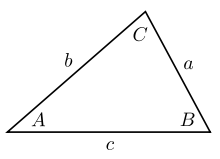
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

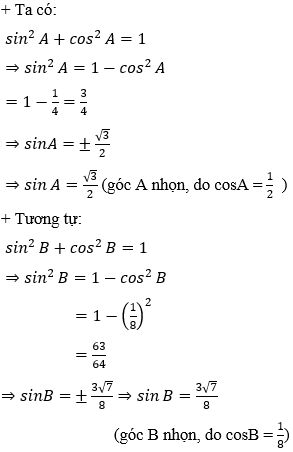
Ví dụ 2: Cho tam giác 

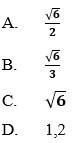
Hướng dẫn giải:

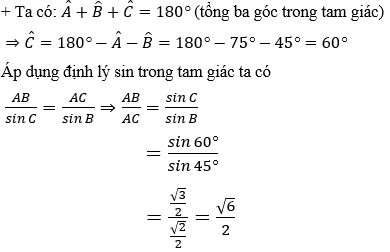
Đáp án A

Ví dụ 3: Cho tam giác ABC có 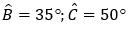 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

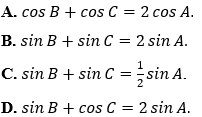
Hướng dẫn giải:

Đáp án B

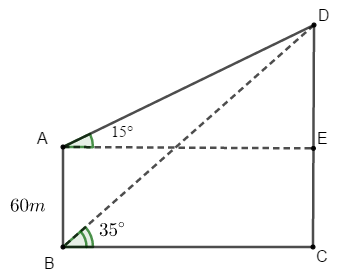
Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

Áp dụng định lý sin trong tam giác ABD ta có:

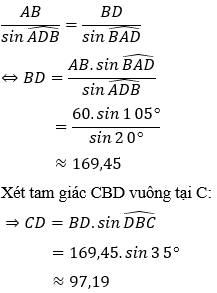
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

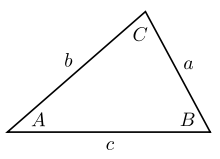
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

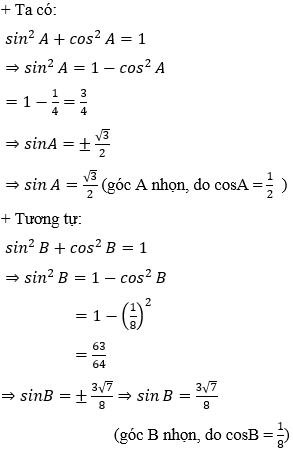
Ví dụ 2: Cho tam giác 

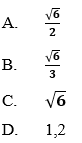
Hướng dẫn giải:

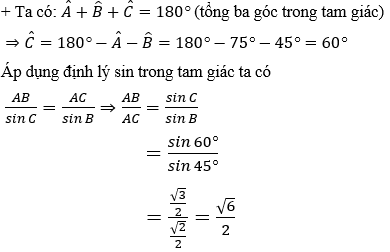
Đáp án A

Ví dụ 3: Cho tam giác ABC có 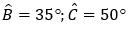 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

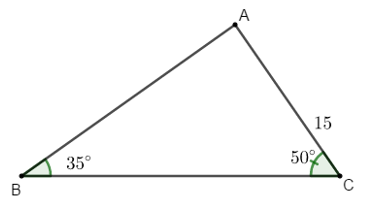
Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

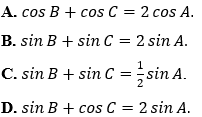
Hướng dẫn giải:

Đáp án B

Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

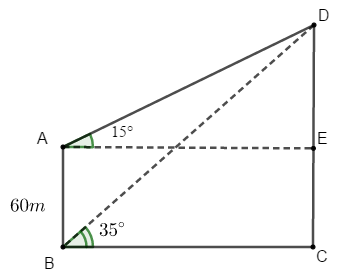
Áp dụng định lý sin trong tam giác ABD ta có:

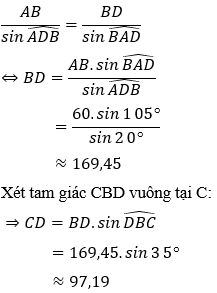
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

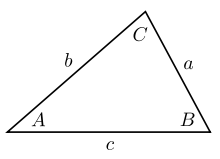
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

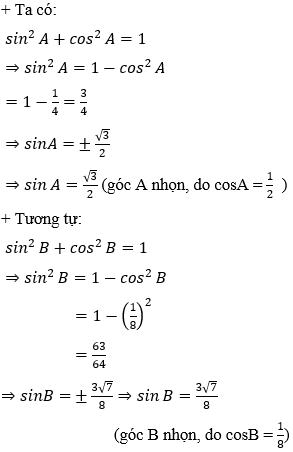
Ví dụ 2: Cho tam giác 

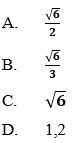
Hướng dẫn giải:

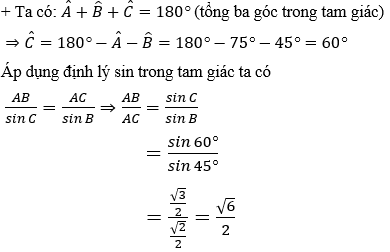
Đáp án A

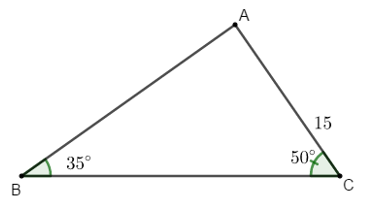
Ví dụ 3: Cho tam giác ABC có 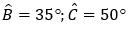 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

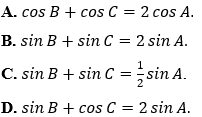
Hướng dẫn giải:

Đáp án B

Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

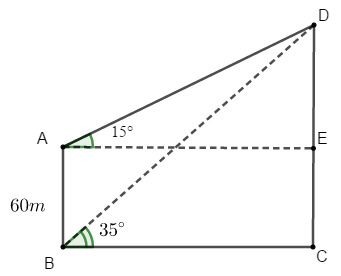
Áp dụng định lý sin trong tam giác ABD ta có:

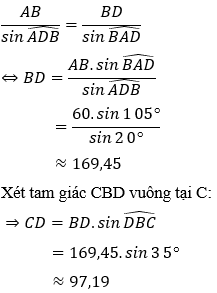
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

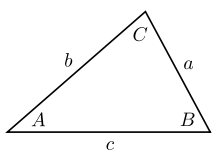
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

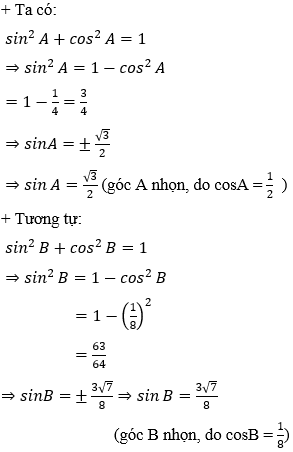
Ví dụ 2: Cho tam giác 

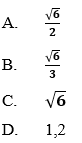
Hướng dẫn giải:

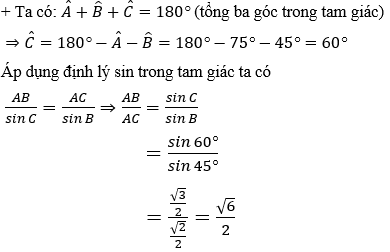
Đáp án A

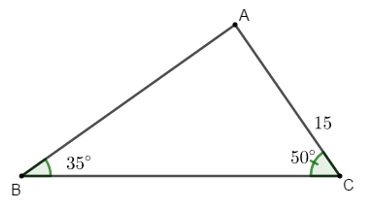
Ví dụ 3: Cho tam giác ABC có 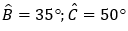 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

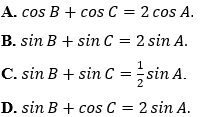
Hướng dẫn giải:

Đáp án B

Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

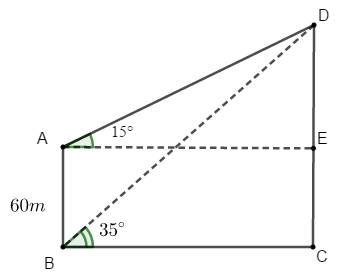
Áp dụng định lý sin trong tam giác ABD ta có:

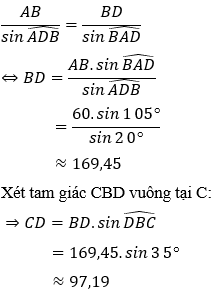
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

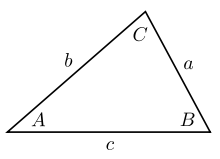
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

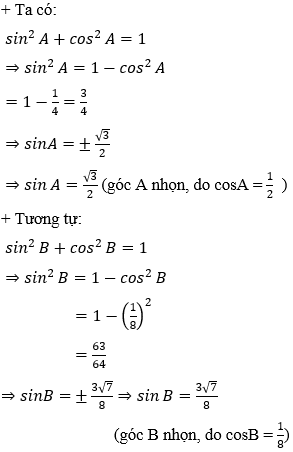
Ví dụ 2: Cho tam giác 

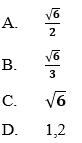
Hướng dẫn giải:

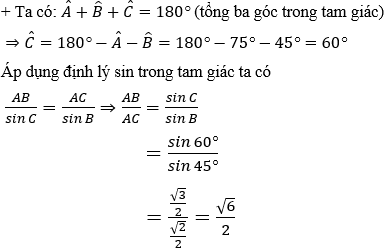
Đáp án A

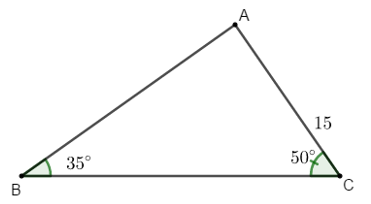
Ví dụ 3: Cho tam giác ABC có 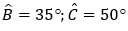 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

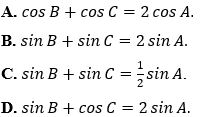
Hướng dẫn giải:

Đáp án B

Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

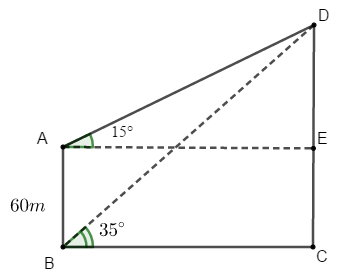
Áp dụng định lý sin trong tam giác ABD ta có:

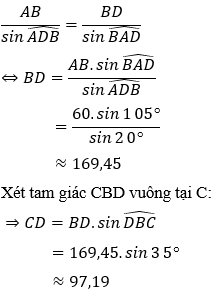
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

Định lí Sin hay công thức Sin, định luật Sin là phần kiến thức Hình học quan trọng học sinh đã được tìm hiểu trong chương trình Toán phổ thông. Nhằm giúp các bạn nắm vững hơn chuyên đề này, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh, Mầm Non Ánh Dương đã chia sẻ bài viết sau đây. Các bạn tìm hiểu nhé !

I. ĐỊNH LÍ SIN LÀ GÌ ?

This post: Định lí Sin trong tam giác là gì? Định lí Sin áp dụng khi nào?

1. Định lí

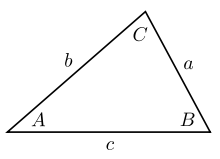
Trong lượng giác, định lý sin (hay định luật sin, công thức sin) là một phương trình biểu diễn mối quan hệ giữa chiều dài các cạnh của một tam giác bất kì với sin của các góc tương ứng. Định lý sin được biểu diễn dưới dạng:

a/sin A = b/sin B = c/sin C

trong đó a, b, c là chiều dài các cạnh, và A, B, C là các góc đối diện (xem hình vẽ). Phương trình cũng có thể được viết dưới dạng nghịch đảo:

SinA/a = SinB/b = SinC/c

Trong một vài trường hợp, khi áp dụng định lý sin, ta được hai giá trị khác nhau, dẫn đến khả năng dựng được hai tam giác khác nhau trong cùng một bài toán giải tam giác.

Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

2. Ví dụ:

Cho: cạnh a = 20, cạnh c = 24, góc C = 40°

Theo định lý sin ta có

Một ví dụ khác:

Nếu hai cạnh của một tam giác có chiều dài là R và chiều dài cạnh thứ ba, dây cung c, là 100, góc C đối diện với dây cung c thì:

và

 

II. CÁCH ÁP DỤNG ĐỊNH LÍ SIN TRONG TAM GIÁC CỰC HAY

Định lý sin có thể được dùng trong phép đạc tam giác để tìm hai cạnh còn lại của một tam giác khi biết một cạnh và hai góc bất kì, hoặc để tìm cạnh thứ ba khi biết hai cạnh và một góc không xen giữa hai cạnh đó.

Trong một vài trường hợp, công thức cho ta hai giá trị khác nhau, dẫn đến hai khả năng khác nhau của một tam giác. Định lý sin là một trong hai phương trình lượng giác thường được dùng để tìm cạnh và góc của một tam giác, ngoài định lý cos.

Ví dụ 1: Cho tam giác ABC có BC = 8, cosA = 1/2 và cosB = 1/8. Tính cạnh AC.

Hướng dẫn giải:

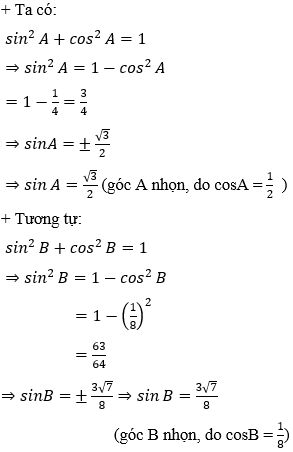
Ví dụ 2: Cho tam giác 

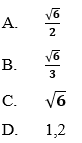
Hướng dẫn giải:

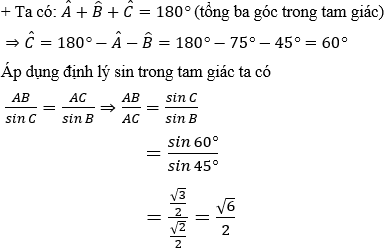
Đáp án A

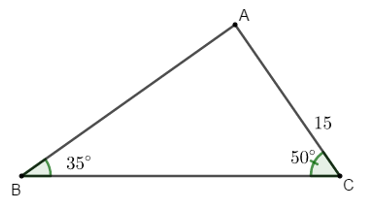
Ví dụ 3: Cho tam giác ABC có 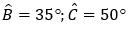 và cạnh AC = 15 cm. Tính các cạnh còn lại của tam giác ABC.

Hướng dẫn giải:

Ví dụ 4: Cho tam giác ABC với BC = a, CA = b và AB = c thỏa mãn b + c = 2a. Đẳng thức nào sau đây đúng?

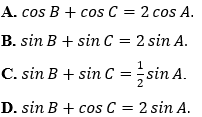
Hướng dẫn giải:

Đáp án B

Ví dụ 5: Một người quan sát đỉnh của một ngọn núi từ hai vị trí khác nhau của tòa nhà. Lần đầu tiên người đó quan sát đỉnh núi từ tầng trệt với phương nhìn tạo với phương nằm ngang một góc 35° và lần thứ hai người này quan sát tại sân thượng của cùng tòa nhà đó với phương nhìn tạo với phương nằm ngang một góc 15°. Tính chiều cao ngọn núi đó so với mặt đất biết rằng tòa nhà cao 60m.

Hướng dẫn giải:

Bài toán trên được mô phỏng lại như hình vẽ với A là vị trí của người đó tại sân thượng của tòa nhà, B là vị trí của người đó tại tầng trệt. C và D lần lượt là đỉnh và chân của ngọn núi.

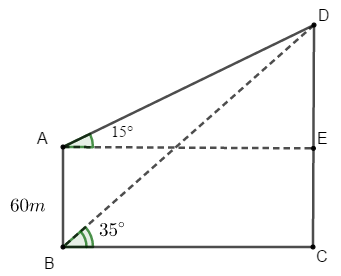
Áp dụng định lý sin trong tam giác ABD ta có:

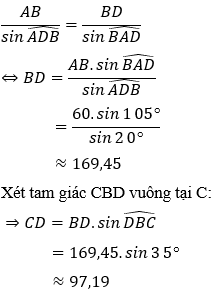
Vậy ngọn núi cao xấp xỉ bằng 97,19 m.

Bài viết trên đây, chúng tôi đã giới thiệu đến quý bạn đọc định lí Sin trong tam giác, về cách áp đụng định lí Sin vào việc tìm cạnh và góc của một tam giác cực nhanh. Hi vọng, những chia sẻ này hữu ích với bạn. Xem thêm công thức tính diện tích tam giác: thường, cân, vuông, đều & các dạng toán thường gặp tại đường link này nhé !

Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục