Công thức tính nguyên hàm và bảng nguyên hàm Đầy Đủ, Chính Xác

Công thức tính nguyên hàm và bảng nguyên hàm Đầy Đủ, Chính Xác

Nguyên hàm là gì? Công thức tính nguyên hàm và bảng nguyên hàm là phần kiến thức quan trọng trong chương trình Giải tích 12 xuất hiện hầu hết trong các đề thi. Bài viết hôm nay, Mầm Non Ánh Dương sẽ hệ thống lại tất cả các kiến thức cần ghi nhớ về chuyên đề nguyên hàm. Các bạn theo dõi nhé !

I. LÝ THUYẾT VỀ NGUYÊN HÀM

This post: Công thức tính nguyên hàm và bảng nguyên hàm Đầy Đủ, Chính Xác

1. Định nghĩa nguyên hàm

Định nghĩa:

• Cho hàm số f(x) xác định trên K.

• Hàm số F(x) được gọi là nguyên hàm của hàm số f(x) trên K nếu F′(x)=f(x) với mọi x∈K.

• Kí hiệu K là khoảng hoặc đoạn hoặc nửa khoảng của R.

2. Định lý nguyên hàm

Định lý:

• Định lý 1: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì với mỗi hằng số C, hàm số G(x)=F(x)+CG(x)=F(x)+C cũng là một nguyên hàm của hàm số f(x) trên K.

• Định lý 2: Nếu F(x) là một nguyên hàm của hàm số f(x) trên K thì mọi nguyên hàm của f(x) trên K đều có dạng F(x)+CF(x)+C với C là một hằng số tùy ý.

• Định lí 3: Mọi hàm số f(x) liên tục trên K đều có nguyên hàm trên K.

Lưu ý: 

• Kí hiệu họ nguyên hàm của hàm số f(x) là ∫f(x)dx

• Khi đó : ∫f(x)dx=F(x)+C,C∈R.

3. Tính chất của nguyên hàm

∫f(x)dx = F(x) + C, C ∈ R.

∫kf(x)dx =k ∫f(x)dx (với k là hằng số khác 0)

∫(f(x) ± g(x)) = ∫f(x)dx ± ∫g(x)dx

II. BẢNG CÔNG THỨC TÍNH NGUYÊN HÀM (TỪ CƠ BẢN ĐẾN NÂNG CAO)

Sau đây chúng tôi sẽ giới thiệu đến quý thầy cô và các bạn học sinh bảng công thức tính nguyên hàm từ cơ bản đến nâng cao, mở rông chi tiết, chính xác nhất. Bạn theo dõi nhé !

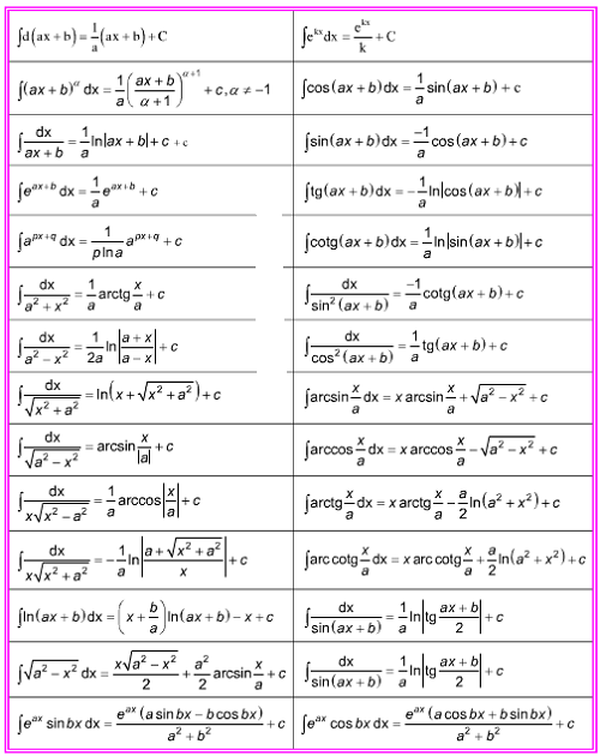
1. Bảng công thức tính nguyên hàm cơ bản

2. Bảng công thức nguyên hàm mở rộng với a # 0

3. Bảng nguyên hàm nâng cao

**** Tổng hợp công thức nguyên hàm cần nhớ

III. CÁC DẠNG TOÁN NGUYÊN HÀM THƯỜNG GẶP 

Dạng 1: Tìm nguyên hàm của hàm số

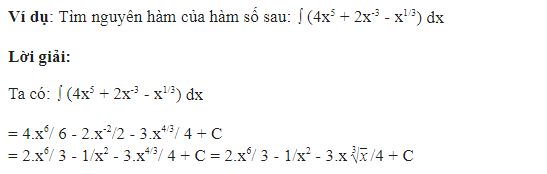
Dạng 2: Tìm nguyên hàm của hàm số bằng phương pháp đổi biến số

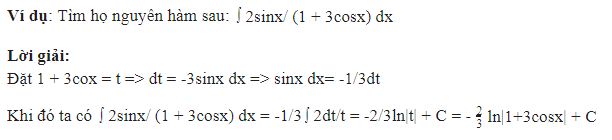
Dạng 3: Tìm nguyên hàm bằng phương pháp từng phần

Dạng 4: Một số bài toán nâng cao khác liên quan đến công thức tính nguyên hàm.

Ví dụ: Tìm họ nguyên hàm của hàm số

a) ∫2xln(x-1)dx

b)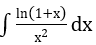 

Hướng dẫn:

a) Xét ∫2xln(x-1)dx

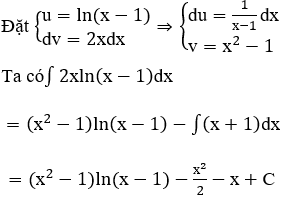
b)

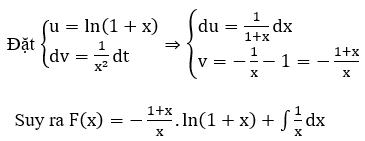
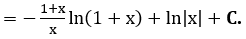
IV. BÀI TẬP VẬN DỤNG

Bài 1: Tìm nguyên hàm của hàm số

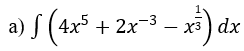
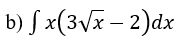
Hướng dẫn:

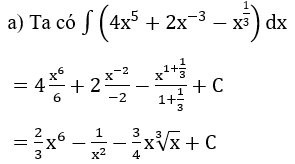
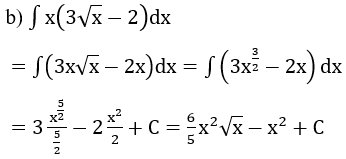
Bài 2: Tìm nguyên hàm của hàm số

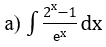
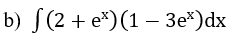
Hướng dẫn:

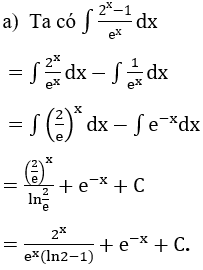
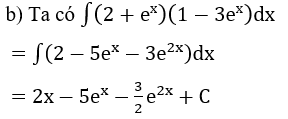
Bài 3: Tìm các họ nguyên hàm sau đây:

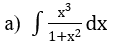
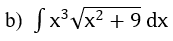
Hướng dẫn:

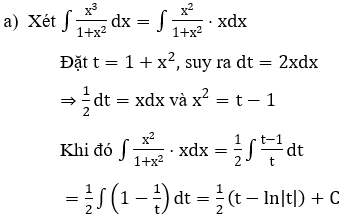
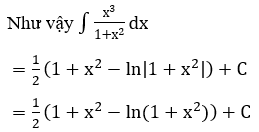
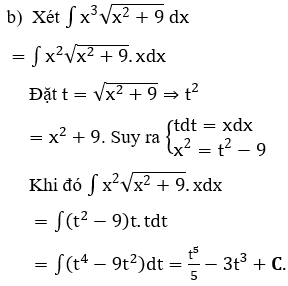
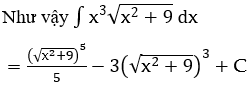
Bài 4: Tìm các họ nguyên hàm sau đây:

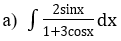
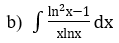
Hướng dẫn:

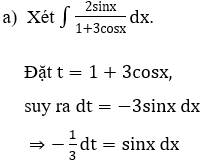
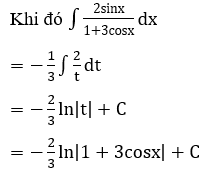
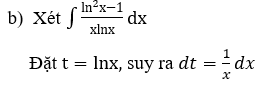
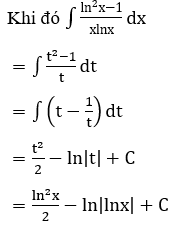
Bài 5: Tìm các họ nguyên hàm sau đây:

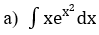
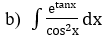
Hướng dẫn:

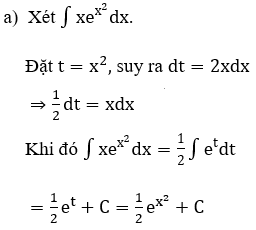
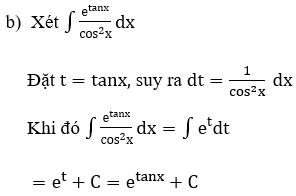
Bài 6: Tìm họ nguyên hàm của hàm số

a) ∫xsinxdx

b) ∫e^x sinx dx

Hướng dẫn:

a) Xét ∫xsinxdx

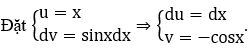
Theo công thức tính nguyên hàm từng phần, ta có

F(x) = ∫xsinxdx = -xcosx+∫cosxdx = -xcosx+sinx+C

b) Xét F(x) = ∫e^x sinx dx

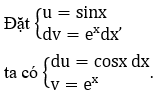
F(x) = e^x sinx-∫e^x cosx dx = e^x sinx-G(x) (1)

Với G(x) = ∫e^x cosx dx

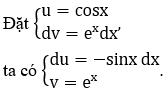
G(x) = e^x cosx+∫e^x sinx dx+C’=e^x cosx+F(x)+C’ (2)

Từ (1) và (2) ta có F(x) = e^x sinx-e^x cosx – F(x) – C’

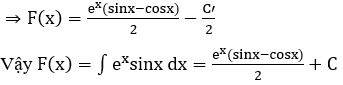
Ghi nhớ: Gặp ∫e^mx+n.sin(ax+b)dx hoặc ∫e^mx+n.cos(ax+b)dx ta luôn thực hiện phương pháp nguyên hàm từng phần 2 lần liên tiếp.

Bài 7: Tìm họ nguyên hàm của hàm số

a) ∫x.2^x dx

b) ∫(x²-1) e^x dx

Hướng dẫn:

a) Xét ∫x.2^x dx

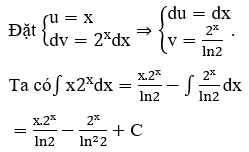
b)

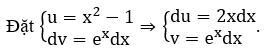
Suy ra ∫f(x)dx = (x²-1) e^x – ∫2x.e^x dx

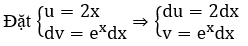
Suy ra ∫f(x)dx = (x²-1) e^x – ∫2x.e^x dx = (x²-1) e^x-(2x.e^x – ∫2.e^x dx)

= (x²-1) e^x – 2x.e^x + 2.e^x+C = (x-1)² e^x + C.

Vậy là các bạn vừa được chia sẻ công thức tính nguyên hàm và bảng nguyên hàm Đầy Đủ, Chính Xác nhất. Hi vọng, sau khi chia sẻ cùng bài viết, bạn nắm vững hơn phần kiến thức Giải tích vô cùng quan trọng này. Xem thêm các bước khảo sát và vẽ đồ thị hàm số bậc 4 nữa bạn nhé !

Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)

Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục