Con lắc đơn là một phần kiến thức nằm trong chương trình môn Vật lý, con lắc đơn được ứng dụng cao trong đời sống, đặc biệt là trong cuộc sống khoa học công nghệ phát triển, được áp dụng vào trong mọi lĩnh vực. Vậy Con lắc đơn có cấu tạo như thế nào? Xin mời các bạn cùng trường Mầm Non Ánh Dương tìm câu trả lời cho câu hỏi Con lắc đơn có cấu tạo như thế nào? cùng với những kiến thức xoay quanh con lắc đơn trong bài viết sau đây nhé!
Con lắc là gì?
Con lắc theo định nghĩa chung nhất là một vật gắn vào một trục cố định mà nó có thể xoay (hay dao động) một cách tự do. Khi đưa con lắc dịch chuyển khỏi vị trí cân bằng theo chiều ngang, nó sẽ chịu một lực phục hồi do tác dụng của hấp dẫn đưa nó trở lại vị trí cân bằng. Khi được thả ra, lực phục hồi kết hợp với trọng lượng của con lắc khiến cho nó dao động xung quanh vị trí cân bằng. Thời gian để con lắc hoàn thiện một lần dao động tới lui gọi là chu kỳ dao động. Chu kỳ dao động phụ thuộc vào độ dài của con lắc cũng như một phần vào biên độ. Tuy nhiên, nếu như biên độ là nhỏ và con lắc không chịu lực cản hay ma sát nào thì chu kỳ dao động độc lập với biên độ con lắc dao động.
This post: Con lắc đơn có cấu tạo như thế nào? Lý thuyết và bài tập
Từ khi được khám phá và nghiên cứu bởi Galileo Galilei vào năm 1602, chuyển động đều của con lắc đã được ứng dụng để đo thời gian và là thiết bị đo thời gian chính xác nhất cho đến thập niên 1930. Đồng hồ quả lắc được Christian Huygens phát minh vào năm 1658 đã trở thành thời gian kế tiêu chuẩn của thế giới, được sử dụng tại gia và văn phòng trong 270 năm và có sai số khoảng một giây mỗi năm trước khi nó được thay thế bởi các đồng hồ thạch anh vào những năm 1930. Con lắc cũng được áp dụng vào các dụng cụ đo đạc khoa học như gia tốc kế và địa chấn kế. Trong lịch sử, chúng còn được sử dụng trong các hấp dẫn kế để đo gia tốc hấp dẫn trong khảo sát địa lý hay thậm chí để làm đơn vị chuẩn của độ dài.
Con lắc đơn có cấu tạo như thế nào?
Cấu tạo của con lắc đơn: Con lắc đơn có cấu tạo rất đơn giản bao gồm: 1 sợi dây (khối lượng rất nhẹ, không đáng kể) với chiều dài l. Dây không dãn. Một đầu của dây gắn vào điểm cố định, đầu dây còn lại gắn với vật có khối lượng m.
Phương trình dao động của con lắc đơn
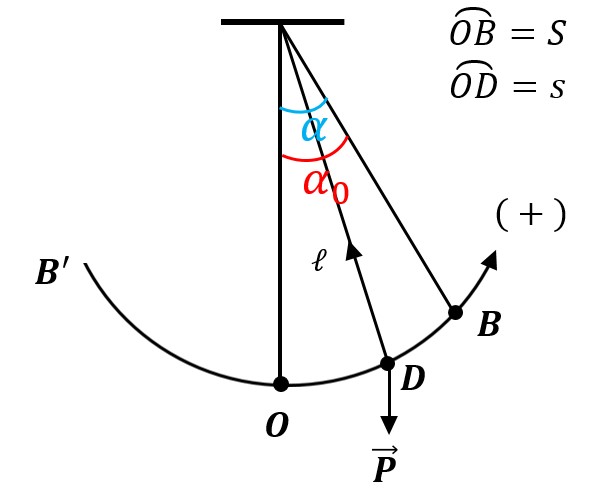
Phương trình dao động của con lắc đơn có dạng:
begin{aligned} &s= Scos(ωt+varphi)\ &α=α_0cos(ωt+varphi)\ &text{Với }s=l.α end{aligned}s=Scos(ωt+φ)α=α0cos(ωt+φ)Với s=l.α
Trong đó:
- s: là cung dao động (Đơn vị tính: cm, m,…)
- S: là biên độ cung (Đơn vị tính: cm, m,…)
- α: là li độ góc (Đơn vị tính: rad)
- α: là biên độ góc (Đơn vị tính: rad)
- ω = gl (rad/s) với g là gia tốc trọng trường (m/s2) và l là chiều dài dây treo (m)
Phương trình vận tốc và gia tốc
v = s’ = – ω.S.sin(ωt + φ) (m/s)
⟹ vmax = ωS
a = v’ = x” = – ω2.S.cos(ωt + φ) (cm/s) = – ω2.s (m/s2)
⟹ amax = ω2.s
Các công thức con lắc đơn lớp 10
Công thức tính chu kỳ và tần số
– Công thức tính tần số góc của con lắc đơn: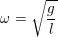 
– Công thức tính chu kì của con lắc đơn: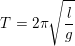 
– Công thức tính tần số của con lắc đơn: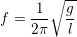 
– Như vậy: khi con lắc đơn dao động điều hòa thì chu kì của nó không phụ thuộc vào khối lượng vật nặng và biên độ.
Công thức tính năng lượng của con lắc đơn
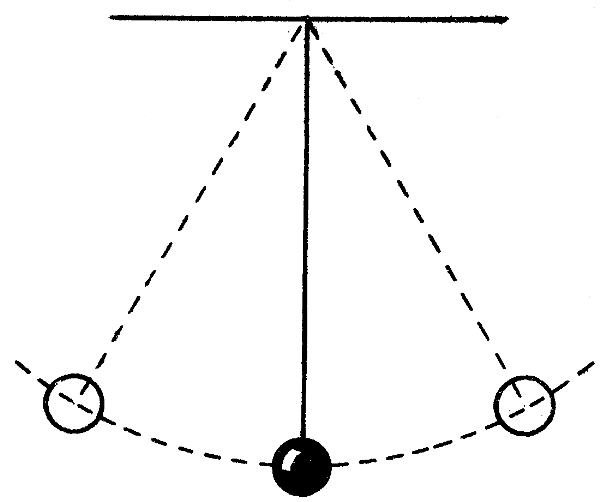
Các công thức tính năng lượng của con lắc đơn dao động điều hòa là:
Động năng của con lắc đơn
– Công thức tính động năng của con lắc đơn:
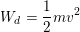
Thế năng của con lắc đơn ở li độ góc α
– Công thức tính thế năng của con lắc đơn:
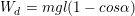(với mốc tính thế năng ở vị trí cân bằng).
Cơ năng của con lắc đơn
– Cơ năng của con lắc đơn được bảo toàn nếu bỏ qua mọi ma sát, công thức tính cơ năng:
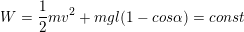(hằng số)
hay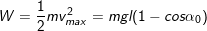 
Lưu ý:
- Nếu bỏ qua ma sát thì cơ năng của con lắc đơn bảo toàn;
- Công thức trên đúng với mọi α ≤ 900.
Công thức tính vận tốc và lực căng dây
Công thức tính vận tốc của con lắc đơn
![Cơ bản - Con lắc đơn [buổi 2] | Tăng Giáp](https://mamnonanhduongvt.edu.vn/wp-content/uploads/2022/11/uir4b4yre63nmcbaym_hub2w-81ntjsby4i_z6axbgw769-h596-no-1.png "uir4b4yre63nmcbaym_hub2w-81ntjsby4i_z6axbgw769-h596-no-1")
Công thức tính lực căng dây của con lắc đơn
Ứng dụng của con lắc đơn: Xác định gia tốc rơi tự do
Trong thực tế, các nhà khoa học ứng dụng con lắc đơn vào việc xác định gia tốc trọng trường của một địa điểm nào đó.
Khi các yếu tố của con lắc như chiều dài l (m) của con lắc, chu kì dao động T (s) của con lắc bằng các phép đo thực nghiệm; ta có thể xác định gia tốc rơi tự do theo công thức:
g=4π2.l / T2
Các dạng bài tập con lắc đơn hay có trong đề thi THPT Quốc Gia Cập Nhật 10/2022
Dạng 1: Bài tập áp dụng công thức chu kì và tần số của con lắc đơn
Ví dụ: Một con lắc đơn có chu kỳ T = 2s. Nếu tăng chiều dài của con lắc thêm 20,5cm thì chu kỳ dao động mới của con lắc là 2,2s. Tìm chiều dài và gia tốc trọng trường g.
Giải: Gọi T và T’ là chu kỳ dao động của con lắc trước và sau khi tăng chiều dài.
Ta có:
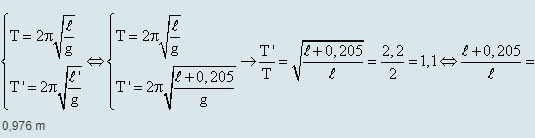
Thay l vào công thức tính T ta có:
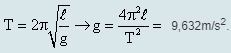
Dạng 2: Tính tốc độ và lực căng dây của con lắc đơn
Ví dụ : Một con lắc đơn có chiều dài dây treo là 100cm, kéo con lắc lệch khỏi VTCB một góc α0 với cosα0 = 0,892 rồi truyền cho nó vận tốc v = 30cm/s. Lấy g = 10m/s2.
a. Tính vmax
b. Vật có khối lượng m = 100g. Hãy tính lực căng dây khi dây treo hợp với phương thẳng đứng góc α với cosα = 0,9
Hướng dẫn giải :
a. Áp dụng công thức tính tốc độ của con lắc đơn ta có:
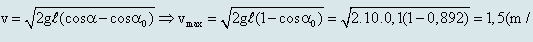
b. Theo công thức tính lực căng dây treo ta có:
Ví dụ 2 : Một con lắc đơn có m = 100g, dao động điều hòa với biên độ góc α0 = 300. Lấy g = 10m/s2. Tính lực căng dây cực tiểu của con lắc trong quá trình dao động.
Giải :
Ta có công thức tính lực căng dây:
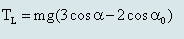
Lực căng dây đạt giá trị cực tiểu khi:
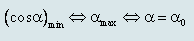
Khi đó:
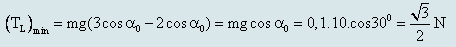
Dạng 3: Lập phương trình dao động của con lắc đơn.
* Chú ý : Khi lập phương trình dao động của con lắc đơn có hai dạng phương trình:
Phương trình dao động theo li độ dài:
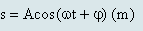
Phương trình dao động theo li độ góc:
Ví dụ : Một con lắc đơn dao động điều hòa có chu kỳ dao động T = 2s. Lấy g = 10m/s2, π2 = 10. Viết phương trình dao động của con lắc biết rằng tại thời điểm ban đầu vật có li độ góc α = 0,05 (rad) và vận tốc v = -15,7 (cm/s).
Giải :
Gọi phương trình dao động theo li độ dài của con lắc là:
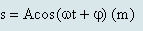
Trong đó:
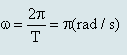
Áp dụng hệ thức liên hệ ta tính được biên độ dài của con lắc đơn:
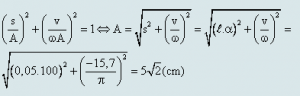
Khi đó tại t = 0 ta có:
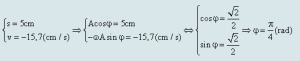
Vậy phương trình dao động của con lắc là:
Ví dụ: Một con lắc đơn dao động điều hòa có chiều dài . Tại t = 0, từ vị trí cân bằng truyền cho con lắc một vận tốc ban đầu 14cm/s theo chiều dương của trục tọa độ. Lấy g = 9,8m/s2, viết phương trình dao động của con lắc.
Giải :
Gọi phương trình dao động theo li độ dài của con lắc là:
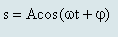
Tần số góc dao động:
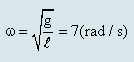
Vận tốc tại vị trí cân bằng là vận tốc cực đại nên ta có:
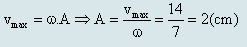
Khi đó tại t = 0 ta có:
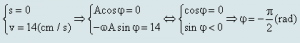
Vậy phương trình dao động của con lắc là:
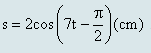
Dạng 4 : Năng lượng dao động của con lắc đơn
Chú ý khi làm bài tập :
– Tính toán năng lượng dao động khi góc lệch lớn (Dao động của con lắc khi này là dao động tuần hoàn chứ không phải dao động điều hòa) :
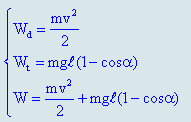
Tính toán năng lượng dao động khi góc lệch nhỏ (lúc này dao động của con lắc là dao động điều hòa, thường thì trong kỳ thi Đại học sẽ là trường hợp này):
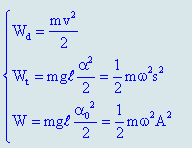
Khi đề bài cho mối quan hệ giữa động năng và thế năng (chẳng hạn cho Wd = k.Wt, với k là một hệ số tỉ lệ nào đó) thì:
+ Tính li độ dài (s) hay li độ góc (α) chúng ta quy hết về theo Thế năng (Wt). Cụ thể như sau:
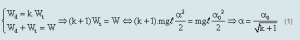
Tương tự để tính tốc độ v thì chúng ta quy hết theo động năng (Wd) :
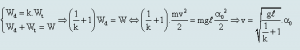
Nhận xét :
– Nhìn biểu thức thì có vẻ phức tạp nhưng thực ra trong bài toán cụ thể chúng ta thực hiện phép giản ước sẽ được biểu thức hay kết quả đẹp hơn nhiều.
– Trong các đề thi để cho việc tính toán đơn giản thì ở (1) thường cho các giá trị của k là k = 1 hoặc k = 3.
Ví dụ : Một con lắc đơn có l=1m, dao động điều hòa tại nơi có g = 10m/s2 và góc lệch cực đại là 90. Chọn gốc thế tại vị trí cân bằng. Giá trị của vận tốc con lắc tại vị trí động năng bằng thế năng là bao nhiêu ?
Giải :
Năng lượng dao động của con lắc đơn là:
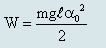
Khi động năng bằng thế năng (tính vận tốc nên nhớ quy về Động năng nhé) ta có:
Bài tập và hướng dẫn giải
Câu 1: SGK Vật lí 12, trang 17:
Thế nào là con lắc đơn? Khảo sát dao động của con lắc đơn về mặt động lực học. Chứng minh rằng dao động nhỏ (sinα≈α (rad)), dao động của con lắc đơn là giao động điều hòa.
Con lắc đơn là một hệ gồm một vật nhỏ khối lượng m, treo ở đầu một sợi dây không dãn, khối lượng không đáng kể, chiều dài l.
Câu 2: SGK Vật lí 12, trang 17:
Viết công thức tính động năng, thế năng, cơ năng của con lắc đơn ở vị trí có góc lệch α bất kì.
Khi con lắc dao động thì động năng và thế năng của con lắc biến đổi như thế nào?
Công thức tính động năng, thế năng, cơ năng của con lắc đơn:
- Động năng: Wđ=12.m.v2
- Thế năng: Wt=m.g.l.(1−cosα)
- Cơ năng: W=12.m.v2+m.g.l.(1−cosα)
Khi con lắc dao động nhỏ và không có ma sát, cơ năng của con lắc được bảo toàn. Nó chỉ biến đổi từ dạng thế năng sang động năng và ngược lại.
Câu 4: SGK Vật lí 12, trang 17:
Hãy chọn câu đúng.
A. T=12π.lg−−√
B. T=12π.gl−−√
C. T=2π.lg−−−−√
D. T=2π.lg
Chọn đáp án D.
Video về con lắc đơn cấu tạo như thế nào?
Kết luận
Bài viết đã cung cấp đến các bạn khái niệm của con lắc đơn cùng với những công thức liên quan đến con lắc đơn, hy vọng đã giúp các bạn có kiến thức tốt để giải các bài tập liên quan. Cảm ơn các bạn đã quan tâm theo dõi!
Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục
