Phương pháp giải nhanh bài toán số phức bằng máy tính Casio
A. Các phép tính thông thường, tính moldun, argument, conjg của 1 số phức hay 1 biểu thức số phức và tính số phức có mũ cao.
Bài toán tổng quát: Cho Z = z1.z2 – z3.z4/z5. Tìm z và tính modun, argument và số phức liên hợp của số phức Z.
Phương pháp giải:
+ Để máy tính ở chế độ Deg không để dưới dạng Rad và vào chế độ số phức Mode 2.
+ Khi đó chữ “i” trong phần ảo sẽ là nút “ENG” và ta thực hiện bấm máy như 1 phép tính bình thường.
Tính Moldun, Argument và số phức liên hợp của số phức Z:
+ Moldun: Ấn shift + hyp. Xuất hiện dấu trị tuyệt đối thì ta nhập biểu thức đó vào trong rồi lấy kết quả.
+ Tính Arg ấn Shift 2 chọn 1. Tính liên hợp ấn shift 2 chọn 2.
B. Tìm căn bậc 2, chuyển số phức về dạng lượng giác và ngược lại.
1. Tìm căn bậc 2 của số phức và tính tổng hệ số của căn đó.
Bài toán tổng quát: Cho số phức z thỏa mãn z = f(a, bi). Tìm 1 căn bậc 2 của số phức và tính tổng, tích hoặc 1 biểu thức của hệ số.
Phương pháp giải:
Cách 1: Đối với việc tìm căn bậc 2 của số phức cách nhanh nhất là ta bình phương các đáp án xem đáp án nào trùng số phức đề cho.
Cách 2: Không vào chế độ Mode 2. Ta để máy ở chế độ Mode 1.
+ Ấn shift + sẽ xuất hiện và ta nhập Pol(phần thực, phần ảo). Lưu ý dấu “,” là shift) sau đó ấn =.
+ Ấn tiếp Shift – sẽ xuất hiện và ta nhập Rec(√X, Y:2) sau đó ấn bằng ta sẽ ra lần lượt là phần thực và phần ảo của số phức.
This post: CÁCH GIẢI NHANH SỐ PHỨC
2. Đưa số phức về dạng lượng giác và ngược lại.
Bài toán tổng quát: Tìm dạng lượng giác (bán kính, góc lượng giác) của số phức thỏa mãn z = f(a, bi).
Phương pháp giải:
+ Ấn shift chọn 4 (r + Ấn = sẽ ra kế quả a Chuyển từ lượng giác về số phức: chuyển về radian:
+ Nhập dạng lượng giác của số phức dưới dạng: bán kính + Ấn shift 2 chọn 4 (a = bi) và lấy kết quả.
3. Các phép toán cơ bản hoặc tính 1 biểu thức lượng giác của số phức.
Làm tương tự như dạng chính tắc của số phức.
C. Phương trình số phức và các bài toán liên quan.
1. Phương trình không chứa tham số.
Bài toán tổng quát: Cho phương trình az^2 + bz + c = 0. Phương trình có nghiệm (số nghiệm) là?
Phương pháp giải:
+ Dùng cho máy Vinacal: Mode 2 vào chế độ phức và giải phương trình số phức như phương trình hàm số như bình thường và nhân được nghiệm phức.
+ Đối với Casio fx: Nhiều phương trình có nghiệm thực nên cách tốt nhất ta sẽ nhập phương trình đề cho vào máy tính và thực hiện Calc đáp án để tìm ra đáp án.
2. Phương trình tìm tham số.
Bài toán tổng quát: Cho phương trình az^2 + bz + c = 0. Biết phương trình có nghiệm zi = Ai. Tìm a, b, c.
Phương pháp giải:
+ Mode 2 và lần lượt thay các hệ số ở đáp án vào đề.
+ Dùng Mode 5 để giải phương trình nếu phương trình nào ra nghiệm như đề cho thì đó là đáp án đúng.
D. Tìm số phức thỏa mãn điều kiện phức tạp và tính tổng, tích … hệ số của số phức
(Ngoài cách hỏi trên còn có thể hỏi: Tìm phần thực, phần ảo hay modun … của số phức thỏa mãn điều kiện đề bài).
Bài toán tổng quát: Cho số phức z = a + bi thỏa mã điều kiện (phức tạp kèm cả liên hợp …). Tìm số phức z?
Phương pháp giải:
+ Nhập điều kiện đề cho vào Casio. Lưu ý thay z = a + bi và liên hợp của z = a – bi.
+ Calc a = 1000 và b = 100.
+ Sau khi ra kết quả là : X + Yi ta sẽ phân tích X và Y theo a và b để được 2 phương trình bậc nhất 2 ẩn để giải tìm ra a và b.
+ Lưu ý: Khi phân tích ưu tiên cho hệ số a nhiều nhất có thể.
+ Sau khi tìm được a, b ta làm nốt yêu cầu của đề.
E. Tìm tập hợp biểu diễn của số phức thỏa mãn điều kiện và hình học số phức.
Bài toán tổng quát: Trên mặt phẳng hệ trục tọa độ Oxy tìm tập hợp biểu diễn của số phức z thỏa mã điều kiện.
Phương pháp giải: Ưu tiên việc sử dụng 2 máy tính để giải:
+ Máy thứ 1 ta nhập điều kiện của đề cho với z và liên hợp z dạng tổng quát.
+ Máy thứ 2 lần lượt các đáp án. Ta lấy 2 điểm thuộc các đáp án.
+ Calc 2 điểm vừa tìm vào điều kiện. Cái nào kết quả ra 0 thì đấy là đáp án đúng.
F. Cặp số (x, y) thỏa mã điều kiện phức, số số phức phù hợp với điều kiện.
Phương pháp giải:
+ Mode 2 và nhập điều kiện đề cho vào Casio, chuyển hết về 1 vế.
+ Calc các đáp án. Đáp án nào ra kết quả là 0 thì đó là đáp án đúng.


Sử dụng máy tính Casio để giải bài toán Số phức
Giải bài tập số phức bằng máy tính casio nhanh và chính xác. Chắc chắn sẽ giúp ích rất nhiều cho phần làm trắc nghiệm môn Toán của học sinh
Câu 1: Tính z=(1+2i)3+(3−i)2z=(1+2i)3+(3−i)2
A. -3+8i B.-3-8i C.3-8i D.3+8i
Dùng máy tính (MODE 2) rồi tính nhé
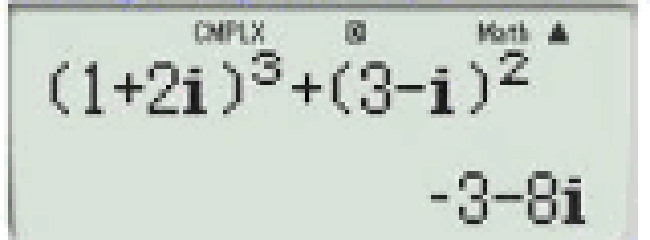
Câu 2: Phần ảo của số phức z=(1−2i)2(3+i)(2+i)z=(1−2i)2(3+i)(2+i)
A.-1/10 B.-7/10 C.-i/10 D.7/10
Dùng máy tính (MODE 2) rồi tính nhé
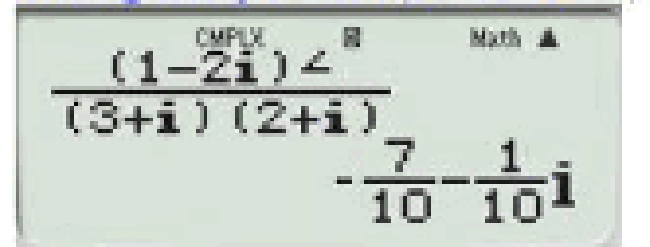
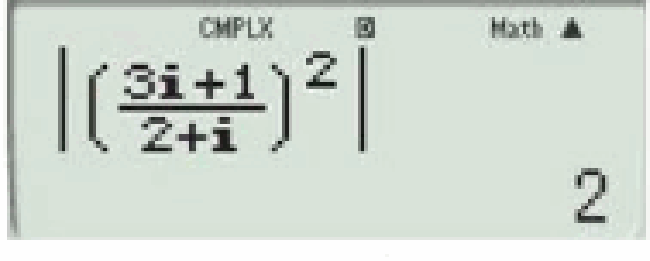
Câu 3: Môdun của số phức z=(3i+12+i)2z=(3i+12+i)2là:
A.4 B.2 C.2i D√22
Dùng máy tính (MODE 2) rồi tính nhé
Môdun là trị tuyệt đối (shift hyp)








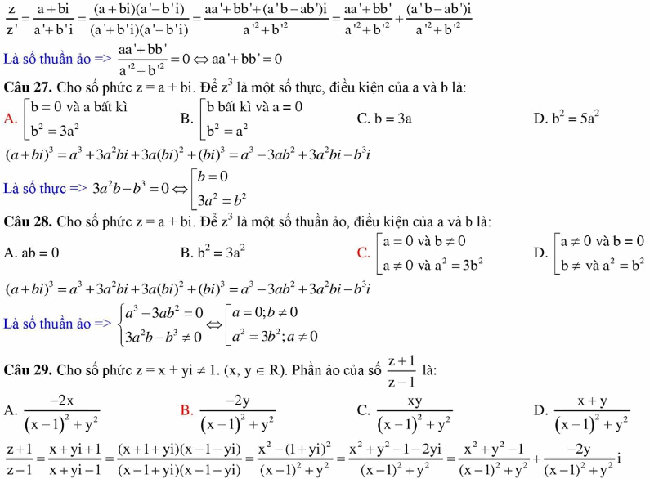


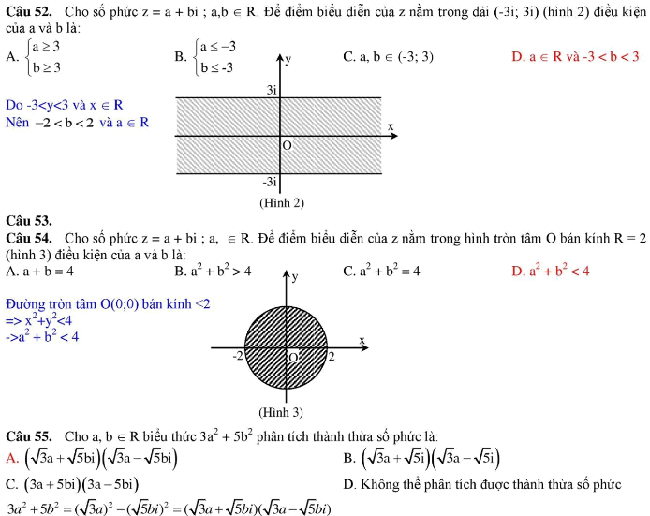
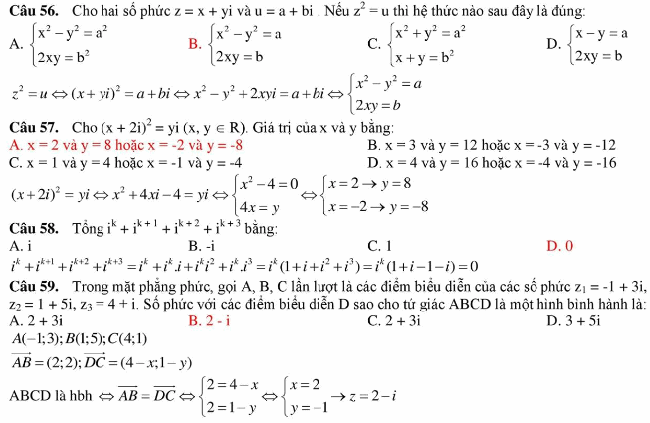

Công thức giải nhanh trắc nghiệm số phức



Mẹo giải bài tập số phức 12 siêu nhanh giúp em đạt điểm cao môn Toán

Khái niệm số phức
Số phức có dạng z = a + bi, (a, b ∈ ℜ), trong đó a là phần thực, b là phần ảo, i là đơn vị ảo: i² = – 1
Tập hợp các số phức là C
Nếu a = 0, z = bi được gọi là số thuần ảo
Nếu b = 0 , z = a + 0i được gọi là số thực
Số 0 vừa là số thực, vừa là số ảo
Số đối của phức z = a + bi là -z = – a – bi
Các phép toán trên tập số phức

Môđun của số phức, số phức liên hợp

Phương trình trên tập số phức


Các dạng bài tập số phức 12 hay và khó
Dạng 1: Các phép toán trên tập hợp số phức

Tìm số phức thỏa mãn điều kiện cho trước


Phương trình trên tập hợp phức

Phương pháp giải nhanh bằng Casino chuyên đề số phức
tất cả các bài toán số phức đều thực hiện trong chức năng MODE 2 (CMPLX) ngoại trừ 1 số bài toán đặc biệt. Chú ý 2 phần D và E
A.. Các phép tính thông thường, tính Moldun, Conjg của 1 số phức hay 1 biểu thức số phức và tính số phức có mũ cao…
Bài toán tổng quát:

Phương pháp giải:
Để máy tính ở chế độ Deg không để dưới dạng Rad và vào chế độ số phức Mode2
Khi đó chữ “i” trong phần ảo sẽ là nút “ENG” và ta thực hiện bấm máy như 1 phép tính bìnhthường.
Tính Moldun và số phức liên hợp của số phức Z:
-> Moldun: Ấn shift + hyp. Xuất hiện dấu trị tuyệt đối thì ta nhập biểu thức đó vào trong rồi lấy kết quả.
Ví dụ 1: Đề thi minh họa của bộ GD&ĐT lần 2 năm 2017.
Tìm số phức liên hợp của số phức z = i(3i + 1)
A: 3-i B: -3+i C: 3+i D: -3-i
Giải: Mode 2 và ấn shift 2, chọn2
Nhập như sau: Conjg(i(3i + 1)) và ấn bằng
Kết quả ra -3 -i, vậy D đúng
Ví dụ 2:Đề thi minh họa của bộ GD&ĐT lần 2 năm 2017

Với số phức có mũ cao thì chỉ máy tính Casio fx 570 vn plus và Vinacal ES plus II có thể bấm được như bình thường. Còn Casio fx 570 es plus thì sẽ Math Error.
B. Tìm căn bậc 2 của số phức
Bài toán tổng quát: Cho số phức z thỏa mãn z = f(a,bi). Tìm 1 căn bậc 2 của số phức và tính tổng, tích hoặc 1 biểu thức của hệ số.
Phương pháp giải:
Cách 1: Đối với việc tìm căn bậc 2 của số phức cách nhanh nhất là ta bình phương các đáp án xem đáp án nào trùng số phức đề cho.
Cách 2: Không vào chế độ Mode 2. Ta để máy ở chế độ Mode1;
Ấn shift + sẽ xuất hiện và ta nhập Pol (phần thực, phần ảo) … Lưu ý dấu “,” là shift ) sau đó ấn =
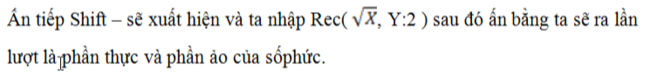
Ví dụ: Tìm 1 căn bậc 2 của số phức: z = (-2 – 6i) + ( 2i –1)
A: -1+2i B: 1 –2i C: 1 + 2i D: -1 – 2i
Giải: Vào mode 2. Rút gọn z về dạng tối giản: z = -3-4i
Lần lượt bình phương các đáp án ta thấy đáp án B khi bình phương sẽ ra đúng đề bài. Nên B đúng
C. Phương trình số phức và các bài toán liên quan
Phương trình không chứa ẩn:
Bài toán tổng quát: Cho phương trình az2+bz+c = 0. Phương trình có nghiệm (số nghiệm) là:
Phương pháp giải:
Dùng cho máy vinacal: Mode 2 vào chế độ phức và giải phương trình số phức như phương trình hàm số như bình thường và nhân được nghiệm phức
Đối với casio fx: Nhiều phương trình có nghiệm thực nên cách tốt nhất ta sẽ nhập phương trình đề cho vào máy tính và thực hiện Calc đáp án để tìm ra đáp án
Phương trình tìm ẩn:ADS BY BLUESEEDSCROLL TO CONTINUE WITH CONTENT
Bài toán tổng quát: Cho phương trình az2+bz+c = 0. Biết phương trình có nghiệm zi = Ai tìm a,b,c …. ?
Phương pháp giải: Mode 2 và lần lượt thay các hệ số ở đáp án vào đề;
Dùng Mode 5 để giải phương trình nếu phương trình nào ra nghiệm như đề cho thì đó là đáp án đúng.
Ví dụ: Phương trình z2 + bz + c = 0 nhận z = 1 + i là nghiệm. Giá trị của b và c là :
A: b = 3;c=5 B: B = 1; c=3 C: b = 4;c=3 D: b = -2;c =2
Giải: Mode 2 và nhập vào máy tính X2 + BX +C
Calc lần lượt cho các đáp án. Khi ta calc cho B = -2, C = 2, X = 1+i ra kết quả bằng 0, vậy D là đáp án đúng.
D. Tìm số phức thỏa mãn điều kiện phức tạp và tính tổng, tích… Hệ số của số phức
Ngoài cách hỏi trên còn có thể hỏi: Tìm phần thực, phần ảo hay moldun….. của số phức thỏa mãn điều kiện đề bài
Bài toán tổng quát: Cho số phức z = a + bi thỏa mã điều kiện ( phức tạp kèm cả liên hợp…) Tìm số phức z?
Phương pháp giải:
Nhập điều kiện đề cho vào casio. Lưu ý thay z = a + bi và liên hợp của z = a –bi
Calc a = 1000 và b =100
Sau khi ra kết quả là : X + Yi ta sẽ phân tích X và Y theo a và b để được 2 phương trình bậc nhất 2 ẩn để giải tìm ra a và b
Lưu ý: Khi phân tích ưu tiên cho hệ số a nhiều nhất có thể ( chú ý ví dụ )
Sau khi tìm được a, b ta làm nốt yêu cầu của đề.
Ví dụ: Tìm phần ảo của số phức z = a + bi biết (1 + i)2.(2 – i)z = 8 + i + (2 + 2i)z
A:-4 B:4 C: 2 D:-2
Giải: Mode 2 và nhập vào casio (1 + i)2.(2 – i)(A+Bi) – 8 – i – (2 +2i)(A+Bi)
Calc A=1000 và B=100
Ta được kết quả là -208 + 1999i.
Phân tích như sau:
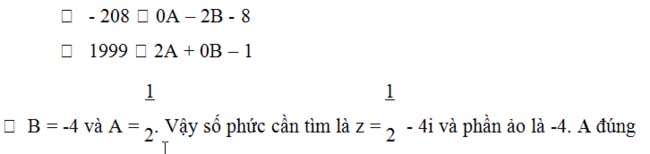
E. Tìm tập hợp biểu diễn của số phức thỏa mãn điều kiện và hình học số phức:
Bài toán tổng quát: Trên mặt phẳng hệ trục tọa độ Oxy tìm tập hợp biểu diễn của số phức z thỏa mã điều kiện…:
Phương pháp giải: Ưu tiên việc sử dụng 2 máy tính để giải
Máy thứ 1 ta nhập điều kiện của đề cho với z và liên hợp z dạng tổng quát
Máy thứ 2 lần lượt các đáp án. Ta lấy 2 điểm thuộc các đáp án
Calc 2 điểm vừa tìm vào điều kiện. Cái nào kết quả ra 0 thì đó là đáp án đúng (chú ý xem ví dụ)
Ví dụ: Trên mặt phẳng Oxy tìm tập hợp biểu diễn các số phức thỏa mã điều kiện |zi – (2 + i)| = 2
A: x + 2y -1=0 B: (x +1)2 + (y – 2)2 =9
C: (x -1)2 + (y + 2)2=4 D: 3x + 4y -2 =0
Giải: Mode 2 và nhập điều kiện vào casio |(A+Bi)i –(2+i)|-2
Thử đáp án A: Cho y = 0 ta được x = 1 ta calc A = 1 và B = 0 kết quả khác 0. Loại luôn đáp án A
Thử đáp án B: Cho x = -1 ta được y = 5. Calc ra kết quả khác 0. Loại đáp án B
Thử đáp án C: cho x = 1 ta được y = 0 và y = -4 Calc lần lượt đều được kết quả bằng 0. Vậy đáp án đúng là C.
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục





