Các dạng bài tập số nguyên, phép toán cộng trừ số nguyên âm cơ bản và nâng cao. Sau khi làm quen với tập số tự nhiên, thì tập số nguyên với các phép toán cộng trừ nhân chia là nội dung kiến thức tiếp theo các em sẽ học. Nếu như số tự nhiên các em mới chỉ biết đến phép trừ của số lớn cho số nhỏ hơn thì ở số nguyên các em có thể thực hiện phép trừ của số nhỏ hơn cho số lớn hơn và được kết quả là số nguyên âm.
Bài viết này chúng ta sẽ tóm tắt lý thuyết về số nguyên, hệ thống một số dạng bài tập về số nguyên, cộng trừ các số nguyên âm qua đó giải các bài tập toán cơ bản và nâng cao về số nguyên để các em nắm vững phần nội dung này.
This post: Các dạng bài tập số nguyên, phép toán cộng trừ số nguyên âm cơ bản và nâng cao – Toán lớp 6
A. Lý thuyết về số nguyên
1. Số nguyên
– Tập hợp: {…; -3 ; -2 ; -1; 0 ; 1; 2; 3;…} gồm các số nguyên âm, số 0 và số nguyên dương là tập hợp các số nguyên.
– Tập hợp các số nguyên được kí hiệu là 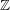 .
.
– Số 0 không phải là số nguyên âm, cũng không phải là số nguyên dương.
2. Giá trị tuyệt đối của một số nguyên
– Khoảng cách từ điểm a đến điểm 0 trên trục số là giá trị tuyệt đối của số nguyên a.
* Ví dụ: |-15| = 15; |9| = 9.
3. Cộng hai số nguyên cùng dấu
– Cộng hai số nguyên dương chính là cộng hai số tự nhiên.
– Muốn cộng hai số nguyên âm, ta cộng hai giá trị tuyệt đối của chúng rồi đặt dấu “-” trước kết quả.
* Ví dụ 1: (+2) + (+5) = 2 + 5 = 7
* Ví dụ 2: (-10) + (-15) = -(10 + 15) = -25
4. Cộng hai số nguyên khác dấu
– Hai số đối nhau có tổng bằng 0.
– Muốn cộng hai số nguyên khác dấu không đối nhau, ta tìm hiệu hai giá trị tuyệt đối của chúng (số lớn trừ số bé) rồi đặt trước kết quả tìm được dấu của số có giá trị tuyệt đối lớn hơn.
* Ví dụ 1: (-3) + (+3) = 0
* Ví dụ 2: (-83) + 42 = – (83 – 42) = -41
5. Tính chất cơ bản của phép cộng số nguyên
– Tính chất giao hoán: a + b = b + a
– Tính chất kết hợp: (a + b) + c = a + (b + c)
– Cộng với số 0: a + 0 = 0 + a = a
– Cộng với số đối : a + (-a) = 0
– Tính chất phân phối : a.(b + c) = a.b + a.c
6. Phép trừ hai số nguyên
– Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b.
a – b = a + (-b)
7. Quy tắc dấu ngoặc
– Khi bỏ dấu ngoặc có dấu “-” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “+” chuyển thành dấu “-” và dấu “-” chuyển thành dấu “+”.
– Khi bỏ dấu ngoặc có dấu “+” đằng trước thì dấu các số hạng trong ngoặc vẫn được giữ nguyên.
* Ví dụ: 36 – (12 + 20 – 9) = 36 – 12 – 20 + 9 = 24 – 20 + 9 = 4 + 9 = 13.
– Khi hình thành ngoặc, nếu ta đặt dấu “-” đằng trước dấu ngoặc thì tất cả các số hạng ban đầu khi cho vào trong ngoặc đều phải đổi dấu. Dấu “-” chuyển thành dấu “+” và dấu “+” chuyển thành dấu “-“.
– Khi hình thành ngoặc, nếu ta đặt dấu “+” đằng trước dấu ngoặc thì tất cả các số hạng bạn đầu khi cho vào trong ngoặc đều phải được giữ nguyên dấu.
* Ví dụ: 105 – 32 – 68 = 105 – (32 + 68) = 105 – 100 = 5.
8. Quy tắc chuyển vế
– Khi chuyển vế mốt số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” chuyển thành dấu “-” và dấu “-” chuyển thành dấu “+”.
A + B + C = D ⇔ A + B = D – C
9. Nhân hai số nguyên
– Muốn nhận hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu “-“ trước kết quả nhận được.
* Ví dụ: 10.(-2) = -20
– Muốn nhân hai số nguyên cùng dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu “+” trước kết quả của chúng.
* Ví dụ: (-6).(-7) = 42
* Nguyên tắc nhớ: Cùng dấu thì Dương, khác dấu thì Âm.
B. Bài tập về số nguyên, các phép toán cộng trừ số nguyên âm
° Dạng 1: So sánh các số nguyên
* Phương pháp:
• Cách 1: Sử dụng trục số:
– Biểu diễn các số nguyên cần so sánh trên trục số;
– Giá trị các số nguyên tăng dần từ trái qua phải.
• Cách 2: Căn cứ vào các nhận xét sau:
– Số nguyên dương lớn hơn 0
– Số nguyên âm nhỏ hơn 0
– Số nguyên dương lớn hơn số nguyên âm
– Trong hai số nguyên dương, số nào có giá trị tuyệt đối lớn hơn thì số ấy lớn hơn;
– Trong hai số nguyên âm, số nào có giá trị tuyệt đối nhỏ hơn thì số ấy lớn hơn.
* Ví dụ 1 (bài 12 trang 73 SGK Toán 6 Tập 1):
a) Sắp xếp các số nguyên sau theo thứ tự tăng dần: 2; -17; 5; 1; -2; 0.
b) Sắp xếp các số nguyên sau theo thứ tự giảm dần: -101; 15; 0; 7; -8; 2001.
* Lời giải (bài 12 trang 73 SGK Toán 6 Tập 1):
a) Dãy số nguyên được sắp xếp theo thứ tự tăng dần là:
–17 < –2 < 0 < 1 < 2 < 5.
b) Dãy số nguyên được sắp xếp theo thứ tự giảm dần là:
2001 > 15 > 7 > 0 > –8 > –101.
* Ví dụ 2: Sắp xếp các số nguyên sau theo thứ tự tăng dần.
5 ; -16 ; 0 ; 25 ;-7 ; -12; 36.
* Lời giải:
– Dãy được sắp xếp tăng dần như sau:
-16 < -12 < -7 < 0 < 5 < 25 < 36
* Ví dụ 3: Sắp xếp các số nguyên sau theo thứ tự giảm dần.
-18 ; -29; 13; 0; 27; 39 ; -103; -3.
* Lời giải:
– Dãy được sắp xếp giảm dần như sau:
39 > 27 > 13 > 0 > -3 > -18 > -29; -103.
* Ví dụ 4 (bài 11 trang 73 SGK Toán 6 Tập 1) : Điền dấu “>” “=” “<” thích hợp vào ô trống (là bài toán so sánh):
a) 3 và 5
b) (-3) và (-5)
c) 4 và (-6)
d) 10 và (-10)
* Lời giải:
a) 3 < 5.
b) So sánh hai số nguyên âm ta so sánh hai giá trị tuyệt đối của chúng. Số nào có giá trị tuyệt đối lớn hơn thì số đó nhỏ hơn.
|-3| = 3 ; |-5| = 5. Mà 3 < 5 nên -3 > -5.
c) Số nguyên dương luôn lớn hơn số nguyên âm: 4 > -6;
d) Số nguyên dương luôn lớn hơn số nguyên âm: 10 > -10.
° Dạng 2: Các phép toán cộng trừ số nguyên
* Phương pháp:
– Áp dụng quy tắc cộng số nguyên cùng dấu, khác dấu, các tính chất giao hoán, kết hợp
* Ví dụ 1 (bài 23 trang 75 SGK Toán 6 Tập 1): Thực hiện phép tính
a) 2763 + 152;
b) (–7) + (–14)
c) (–35) + (–9).
* Lời giải ví dụ 1 (bài 23 trang 75 SGK Toán 6 Tập 1):
a) 2763 + 152 = 2915
b) Ta có : |-7| = 7; |-14| = 14.
Do đó: (-7) + (-14) = – (|-7| + |-14| ) = -(7 + 14) = -21.
c) (-35) + (-9) = -(|-35| + |-9|) = -(35 + 9) = -44.
* Ví dụ 2 (bài 24 trang 75 SGK Toán 6 Tập 1): Tính
a) (-5) + (-248)
b) 17 + |-33|
c) |-37| + |+15|
* Lời giải ví dụ 2 (bài 24 trang 75 SGK Toán 6 Tập 1):
a) (–5) + (–248) = – (5 + 248) = –253;
b) |–33| = 33. Do đó: 17 + |–33| = 17 + 33 = 50
c) |–37| = 37; |15| = 15. Do đó : |–37| + |15| = 37 + 15 = 52.
* Ví dụ 3 (bài 26 trang 75 SGK Toán 6 Tập 1): Nhiệt độ hiện tại của phòng ướp lạnh là -5oC. Nhiệt độ tại đó sẽ là bao nhiêu độ C nếu nhiệt độ giảm 7oC.
* Lời giải ví dụ 3 (bài 26 trang 75 SGK Toán 6 Tập 1):
– Nhiệt độ giảm 7ºC tức là nhiệt độ tăng thêm –7ºC. Vậy nhiệt độ sau khi tăng thêm –7ºC là: (–5) + (–7) = –(5 +7) = –12ºC.
° Dạng 3: Phép toán nhân các số nguyên
* Phương pháp:
– Áp dụng quy tắc nhân số nguyên, các tính chất giao hoán kết hợp và phân phối để tính toán
* Ví dụ 1 (bài 73 trang 89 SGK Toán 6 Tập 1): Thực hiện phép tính:
a) (-5).6 b) 9.(-3) c) (-10).11 d) 150.(-4)
* Lời giải ví dụ 1 (bài 73 trang 89 SGK Toán 6 Tập 1):
a) (-5).6 = -(|-5|.|6|) = -(5.6) = -30.
b) 9.(-3) = -(|9|.|-3|) = -(9.3) = -27.
c) (-10).11 = -(|-10|.|11|) = -(10.11) = -110.
d) 150.(-4) =-(|150|.|-4|) = -(150.4) = -600.
° Dạng 4: Tìm giá trị của x thỏa mãn biểu thức số nguyên
* Phương pháp:
– Vận dụng các tính chất và phép toán cộng trừ nhân chia, đổi dấu, chuyển vế
* Ví dụ 1 (bài 61 trang 87 SGK Toán 6 Tập 1): Tìm số nguyên x, biết:
a) 7 – x = 8 – (-7);
b) x – 8 = (-3) – 8
* Lời giải ví dụ 1 (bài 61 trang 87 SGK Toán 6 Tập 1):
a) 7 – x = 8 – (–7)
7 – x = 8 + 7 (bỏ dấu ngoặc phía trước có dấu –)
7 – 7 – 8 = x (chuyển 8 và 7 từ VP sang VT, chuyển –x từ VT sang VP)
–8 = x
⇒ Vậy x = –8
b) x – 8 = (–3) – 8
x = (–3) – 8 + 8 (chuyển –8 từ vế trái sang vế phải)
x = –3 + 8 – 8
x = –3.
⇒ Vậy x = –3.
* Ví dụ 2 (bài 62 trang 87 SGK Toán 6 Tập 1): Tìm số nguyên a, biết:
a) |a| = 2;
b) |a + 2| = 0
* Lời giải ví dụ 2 (bài 62 trang 87 SGK Toán 6 Tập 1):
a) Có hai số có giá trị tuyệt đối bằng 2 là 2 và –2.
|a| = 2 ⇒ a = –2 hoặc a = 2.
b) Có duy nhất một số có giá trị tuyệt đối bằng 0 là 0.
|a + 2| = 0
a + 2 = 0
a = –2.
* Ví dụ 3 (bài 63 trang 87 SGK Toán 6 Tập 1): Tìm số nguyên x, biết rằng tổng của ba số là 3; -2 và x bằng 5.
* Lời giải ví dụ 3 (bài 63 trang 87 SGK Toán 6 Tập 1):
-Tổng của ba số: 3; –2 và x bằng 5, nên ta có:
3 + (–2) + x = 5
3 – 2 + x = 5
1 + x = 5
x = 5 – 1
x = 4.
* Ví dụ 4 (bài 64 trang 87 SGK Toán 6 Tập 1): Cho a ∈ Z. Tìm số nguyên x, biết:
a) a + x = 5
b) a – x = 2
* Lời giải ví dụ 4 (bài 64 trang 87 SGK Toán 6 Tập 1):
– Lưu ý, đối với bài toán này, a là một số nguyên bình thường, x là số chưa biết cần tìm.
a) a + x = 5
x = 5 – a (chuyển a từ VT sang VP)
b) a – x = 2
a – 2 = x (chuyển 2 từ VP sang VT và chuyển –x từ VT sang VP).
x = a – 2
♦ Ví dụ 5 (bài 65 trang 87 SGK Toán 6 Tập 1): Cho a, b ∈ Z. Tìm số nguyên x, biết:
a) a + x = b
b) a – x = b
* Lời giải ví dụ 5 (bài 65 trang 87 SGK Toán 6 Tập 1):
– Lưu ý, đối với bài toán này, a và b là một số nguyên bình thường, x là số chưa biết cần tìm.
a) a + x = b
x = b – a (chuyển a từ VT sang VP).
b) a – x = b
a – b = x (chuyển –x từ VT sang VP, chuyển b từ VP sang VT)
x = a – b.
° Dạng 5: Ước và Bội của số nguyên
* Phương pháp:
• Tìm các bội của một số nguyên: Dạng tổng quát của số nguyên a là a.m (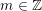 ).
).
• Tìm các ước của số nguyên:
– Nếu số nguyên đã cho có giá trị tuyệt đối nhỏ, ta có thể nhẩm xem nó chia hết cho những số
nào tìm ước của nó, lưu ý nêu đủ các ước âm và ước dương.
– Nếu số nguyên đã cho giá trị tuyệt đối lớn, ta thường phân tích số đó ra thừa số nguyên tố rồi
từ đó tìm tất cả các ước của số đã cho.
* Ví dụ 1 (bài 101 trang 97 SGK Toán 6 Tập 1): Tìm năm bội của: 3; -3.
° Lời giải ví dụ 1 (bài 101 trang 97 SGK Toán 6 Tập 1):
◊ Để tìm bội của số nguyên a, ta nhân a với số nguyên bất kì.
– Năm bội của 3 là: 0; 3; –3; 6; –6;
– Năm bội của –3 là: 0 3; –3; 6; –6;
* Ví dụ 2 (bài 102 trang 97 SGK Toán 6 Tập 1): Tìm tất cả các ước của: -3; 6; 11; -1.
° Lời giải ví dụ 2 (bài 102 trang 97 SGK Toán 6 Tập 1):
– Nhận thấy nếu số nguyên b là ước của số nguyên a thì –b cũng là ước của số nguyên a.
– Đồng thời b là ước của a thì b cũng là ước của |a| và ngược lại.
⇒ Như vậy, để tìm các ước của một số nguyên a, ta chỉ cần tìm các ước dương của |a| rồi thêm các số đối của chúng thì ta được các ước của số nguyên a.
– Các ước dương của 3 là: 1; 3.
⇒ Ư(–3) = {1; 3; –1; –3}
– Các ước dương của 6 là: 1 ; 2 ; 3 ; 6.
⇒ Ư(6) = {1 ; 2 ; 3 ; 6 ; –1; –2; –3; –6}
– Các ước dương của 11 là : 1 ; 11
⇒ Ư(11) = {1 ; 11 ; –1; –11}
– Các ước dương của 1 là 1.
⇒ Ư(–1) = {1; –1}
Hy vọng một số dạng bài tập số nguyên, phép toán cộng trừ số nguyên âm cơ bản và nâng cao ở trên hữu ích cho các em trong việc học tập. Mọi góp ý và có câu hỏi nào các em hãy để lại bình luận dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt.
Các dạng bài tập số nguyên, phép toán cộng trừ số nguyên âm cơ bản và nâng cao
Các dạng bài tập số nguyên, phép toán cộng trừ số nguyên âm cơ bản và nâng cao. Sau khi làm quen với tập số tự nhiên, thì tập số nguyên với các phép toán cộng trừ nhân chia là nội dung kiến thức tiếp theo các em sẽ học. Nếu như số tự nhiên các em mới chỉ biết đến phép trừ của số lớn cho số nhỏ hơn thì ở số nguyên các em có thể thực hiện phép trừ của số nhỏ hơn cho số lớn hơn và được kết quả là số nguyên âm. Bài viết này chúng ta sẽ tóm tắt lý thuyết về số nguyên, hệ thống một số dạng bài tập về số nguyên, cộng trừ các số nguyên âm qua đó giải các bài tập toán cơ bản và nâng cao về số nguyên để các em nắm vững phần nội dung này. A. Lý thuyết về số nguyên 1. Số nguyên – Tập hợp: {…; -3 ; -2 ; -1; 0 ; 1; 2; 3;…} gồm các số nguyên âm, số 0 và số nguyên dương là tập hợp các số nguyên. – Tập hợp các số nguyên được kí hiệu là . – Số 0 không phải là số nguyên âm, cũng không phải là số nguyên dương. 2. Giá trị tuyệt đối của một số nguyên – Khoảng cách từ điểm a đến điểm 0 trên trục số là giá trị tuyệt đối của số nguyên a. * Ví dụ: |-15| = 15; |9| = 9. 3. Cộng hai số nguyên cùng dấu – Cộng hai số nguyên dương chính là cộng hai số tự nhiên. – Muốn cộng hai số nguyên âm, ta cộng hai giá trị tuyệt đối của chúng rồi đặt dấu “-” trước kết quả. * Ví dụ 1: (+2) + (+5) = 2 + 5 = 7 * Ví dụ 2: (-10) + (-15) = -(10 + 15) = -25 4. Cộng hai số nguyên khác dấu – Hai số đối nhau có tổng bằng 0. – Muốn cộng hai số nguyên khác dấu không đối nhau, ta tìm hiệu hai giá trị tuyệt đối của chúng (số lớn trừ số bé) rồi đặt trước kết quả tìm được dấu của số có giá trị tuyệt đối lớn hơn. * Ví dụ 1: (-3) + (+3) = 0 * Ví dụ 2: (-83) + 42 = – (83 – 42) = -41 5. Tính chất cơ bản của phép cộng số nguyên – Tính chất giao hoán: a + b = b + a – Tính chất kết hợp: (a + b) + c = a + (b + c) – Cộng với số 0: a + 0 = 0 + a = a – Cộng với số đối : a + (-a) = 0 – Tính chất phân phối : a.(b + c) = a.b + a.c 6. Phép trừ hai số nguyên – Muốn trừ số nguyên a cho số nguyên b, ta cộng a với số đối của b. a – b = a + (-b) 7. Quy tắc dấu ngoặc – Khi bỏ dấu ngoặc có dấu “-” đằng trước, ta phải đổi dấu tất cả các số hạng trong dấu ngoặc: dấu “+” chuyển thành dấu “-” và dấu “-” chuyển thành dấu “+”. – Khi bỏ dấu ngoặc có dấu “+” đằng trước thì dấu các số hạng trong ngoặc vẫn được giữ nguyên. * Ví dụ: 36 – (12 + 20 – 9) = 36 – 12 – 20 + 9 = 24 – 20 + 9 = 4 + 9 = 13. – Khi hình thành ngoặc, nếu ta đặt dấu “-” đằng trước dấu ngoặc thì tất cả các số hạng ban đầu khi cho vào trong ngoặc đều phải đổi dấu. Dấu “-” chuyển thành dấu “+” và dấu “+” chuyển thành dấu “-“. – Khi hình thành ngoặc, nếu ta đặt dấu “+” đằng trước dấu ngoặc thì tất cả các số hạng bạn đầu khi cho vào trong ngoặc đều phải được giữ nguyên dấu. * Ví dụ: 105 – 32 – 68 = 105 – (32 + 68) = 105 – 100 = 5. 8. Quy tắc chuyển vế – Khi chuyển vế mốt số hạng từ vế này sang vế kia của một đẳng thức, ta phải đổi dấu số hạng đó: dấu “+” chuyển thành dấu “-” và dấu “-” chuyển thành dấu “+”. A + B + C = D ⇔ A + B = D – C 9. Nhân hai số nguyên – Muốn nhận hai số nguyên khác dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu “-“ trước kết quả nhận được. * Ví dụ: 10.(-2) = -20 – Muốn nhân hai số nguyên cùng dấu, ta nhân hai giá trị tuyệt đối của chúng rồi đặt dấu “+” trước kết quả của chúng. * Ví dụ: (-6).(-7) = 42 * Nguyên tắc nhớ: Cùng dấu thì Dương, khác dấu thì Âm. B. Bài tập về số nguyên, các phép toán cộng trừ số nguyên âm ° Dạng 1: So sánh các số nguyên * Phương pháp: • Cách 1: Sử dụng trục số: – Biểu diễn các số nguyên cần so sánh trên trục số; – Giá trị các số nguyên tăng dần từ trái qua phải. • Cách 2: Căn cứ vào các nhận xét sau: – Số nguyên dương lớn hơn 0 – Số nguyên âm nhỏ hơn 0 – Số nguyên dương lớn hơn số nguyên âm – Trong hai số nguyên dương, số nào có giá trị tuyệt đối lớn hơn thì số ấy lớn hơn; – Trong hai số nguyên âm, số nào có giá trị tuyệt đối nhỏ hơn thì số ấy lớn hơn. * Ví dụ 1 (bài 12 trang 73 SGK Toán 6 Tập 1): a) Sắp xếp các số nguyên sau theo thứ tự tăng dần: 2; -17; 5; 1; -2; 0. b) Sắp xếp các số nguyên sau theo thứ tự giảm dần: -101; 15; 0; 7; -8; 2001. * Lời giải (bài 12 trang 73 SGK Toán 6 Tập 1): a) Dãy số nguyên được sắp xếp theo thứ tự tăng dần là: –17 < –2 < 0 < 1 < 2 < 5. b) Dãy số nguyên được sắp xếp theo thứ tự giảm dần là: 2001 > 15 > 7 > 0 > –8 > –101. * Ví dụ 2: Sắp xếp các số nguyên sau theo thứ tự tăng dần. 5 ; -16 ; 0 ; 25 ;-7 ; -12; 36. * Lời giải: – Dãy được sắp xếp tăng dần như sau: -16 < -12 < -7 < 0 < 5 < 25 < 36 * Ví dụ 3: Sắp xếp các số nguyên sau theo thứ tự giảm dần. -18 ; -29; 13; 0; 27; 39 ; -103; -3. * Lời giải: – Dãy được sắp xếp giảm dần như sau: 39 > 27 > 13 > 0 > -3 > -18 > -29; -103. * Ví dụ 4 (bài 11 trang 73 SGK Toán 6 Tập 1) : Điền dấu “>” “=” “<” thích hợp vào ô trống (là bài toán so sánh): a) 3 và 5 b) (-3) và (-5) c) 4 và (-6) d) 10 và (-10) * Lời giải: a) 3 < 5. b) So sánh hai số nguyên âm ta so sánh hai giá trị tuyệt đối của chúng. Số nào có giá trị tuyệt đối lớn hơn thì số đó nhỏ hơn. |-3| = 3 ; |-5| = 5. Mà 3 < 5 nên -3 > -5. c) Số nguyên dương luôn lớn hơn số nguyên âm: 4 > -6; d) Số nguyên dương luôn lớn hơn số nguyên âm: 10 > -10. ° Dạng 2: Các phép toán cộng trừ số nguyên * Phương pháp: – Áp dụng quy tắc cộng số nguyên cùng dấu, khác dấu, các tính chất giao hoán, kết hợp * Ví dụ 1 (bài 23 trang 75 SGK Toán 6 Tập 1): Thực hiện phép tính a) 2763 + 152; b) (–7) + (–14) c) (–35) + (–9). * Lời giải ví dụ 1 (bài 23 trang 75 SGK Toán 6 Tập 1): a) 2763 + 152 = 2915 b) Ta có : |-7| = 7; |-14| = 14. Do đó: (-7) + (-14) = – (|-7| + |-14| ) = -(7 + 14) = -21. c) (-35) + (-9) = -(|-35| + |-9|) = -(35 + 9) = -44. * Ví dụ 2 (bài 24 trang 75 SGK Toán 6 Tập 1): Tính a) (-5) + (-248) b) 17 + |-33| c) |-37| + |+15| * Lời giải ví dụ 2 (bài 24 trang 75 SGK Toán 6 Tập 1): a) (–5) + (–248) = – (5 + 248) = –253; b) |–33| = 33. Do đó: 17 + |–33| = 17 + 33 = 50 c) |–37| = 37; |15| = 15. Do đó : |–37| + |15| = 37 + 15 = 52. * Ví dụ 3 (bài 26 trang 75 SGK Toán 6 Tập 1): Nhiệt độ hiện tại của phòng ướp lạnh là -5oC. Nhiệt độ tại đó sẽ là bao nhiêu độ C nếu nhiệt độ giảm 7oC. * Lời giải ví dụ 3 (bài 26 trang 75 SGK Toán 6 Tập 1): – Nhiệt độ giảm 7ºC tức là nhiệt độ tăng thêm –7ºC. Vậy nhiệt độ sau khi tăng thêm –7ºC là: (–5) + (–7) = –(5 +7) = –12ºC. ° Dạng 3: Phép toán nhân các số nguyên * Phương pháp: – Áp dụng quy tắc nhân số nguyên, các tính chất giao hoán kết hợp và phân phối để tính toán * Ví dụ 1 (bài 73 trang 89 SGK Toán 6 Tập 1): Thực hiện phép tính: a) (-5).6 b) 9.(-3) c) (-10).11 d) 150.(-4) * Lời giải ví dụ 1 (bài 73 trang 89 SGK Toán 6 Tập 1): a) (-5).6 = -(|-5|.|6|) = -(5.6) = -30. b) 9.(-3) = -(|9|.|-3|) = -(9.3) = -27. c) (-10).11 = -(|-10|.|11|) = -(10.11) = -110. d) 150.(-4) =-(|150|.|-4|) = -(150.4) = -600. ° Dạng 4: Tìm giá trị của x thỏa mãn biểu thức số nguyên * Phương pháp: – Vận dụng các tính chất và phép toán cộng trừ nhân chia, đổi dấu, chuyển vế * Ví dụ 1 (bài 61 trang 87 SGK Toán 6 Tập 1): Tìm số nguyên x, biết: a) 7 – x = 8 – (-7); b) x – 8 = (-3) – 8 * Lời giải ví dụ 1 (bài 61 trang 87 SGK Toán 6 Tập 1): a) 7 – x = 8 – (–7) 7 – x = 8 + 7 (bỏ dấu ngoặc phía trước có dấu –) 7 – 7 – 8 = x (chuyển 8 và 7 từ VP sang VT, chuyển –x từ VT sang VP) –8 = x ⇒ Vậy x = –8 b) x – 8 = (–3) – 8 x = (–3) – 8 + 8 (chuyển –8 từ vế trái sang vế phải) x = –3 + 8 – 8 x = –3. ⇒ Vậy x = –3. * Ví dụ 2 (bài 62 trang 87 SGK Toán 6 Tập 1): Tìm số nguyên a, biết: a) |a| = 2; b) |a + 2| = 0 * Lời giải ví dụ 2 (bài 62 trang 87 SGK Toán 6 Tập 1): a) Có hai số có giá trị tuyệt đối bằng 2 là 2 và –2. |a| = 2 ⇒ a = –2 hoặc a = 2. b) Có duy nhất một số có giá trị tuyệt đối bằng 0 là 0. |a + 2| = 0 a + 2 = 0 a = –2. * Ví dụ 3 (bài 63 trang 87 SGK Toán 6 Tập 1): Tìm số nguyên x, biết rằng tổng của ba số là 3; -2 và x bằng 5. * Lời giải ví dụ 3 (bài 63 trang 87 SGK Toán 6 Tập 1): -Tổng của ba số: 3; –2 và x bằng 5, nên ta có: 3 + (–2) + x = 5 3 – 2 + x = 5 1 + x = 5 x = 5 – 1 x = 4. * Ví dụ 4 (bài 64 trang 87 SGK Toán 6 Tập 1): Cho a ∈ Z. Tìm số nguyên x, biết: a) a + x = 5 b) a – x = 2 * Lời giải ví dụ 4 (bài 64 trang 87 SGK Toán 6 Tập 1): – Lưu ý, đối với bài toán này, a là một số nguyên bình thường, x là số chưa biết cần tìm. a) a + x = 5 x = 5 – a (chuyển a từ VT sang VP) b) a – x = 2 a – 2 = x (chuyển 2 từ VP sang VT và chuyển –x từ VT sang VP). x = a – 2 ♦ Ví dụ 5 (bài 65 trang 87 SGK Toán 6 Tập 1): Cho a, b ∈ Z. Tìm số nguyên x, biết: a) a + x = b b) a – x = b * Lời giải ví dụ 5 (bài 65 trang 87 SGK Toán 6 Tập 1): – Lưu ý, đối với bài toán này, a và b là một số nguyên bình thường, x là số chưa biết cần tìm. a) a + x = b x = b – a (chuyển a từ VT sang VP). b) a – x = b a – b = x (chuyển –x từ VT sang VP, chuyển b từ VP sang VT) x = a – b. ° Dạng 5: Ước và Bội của số nguyên * Phương pháp: • Tìm các bội của một số nguyên: Dạng tổng quát của số nguyên a là a.m (). • Tìm các ước của số nguyên: – Nếu số nguyên đã cho có giá trị tuyệt đối nhỏ, ta có thể nhẩm xem nó chia hết cho những số nào tìm ước của nó, lưu ý nêu đủ các ước âm và ước dương. – Nếu số nguyên đã cho giá trị tuyệt đối lớn, ta thường phân tích số đó ra thừa số nguyên tố rồi từ đó tìm tất cả các ước của số đã cho. * Ví dụ 1 (bài 101 trang 97 SGK Toán 6 Tập 1): Tìm năm bội của: 3; -3. ° Lời giải ví dụ 1 (bài 101 trang 97 SGK Toán 6 Tập 1): ◊ Để tìm bội của số nguyên a, ta nhân a với số nguyên bất kì. – Năm bội của 3 là: 0; 3; –3; 6; –6; – Năm bội của –3 là: 0 3; –3; 6; –6; * Ví dụ 2 (bài 102 trang 97 SGK Toán 6 Tập 1): Tìm tất cả các ước của: -3; 6; 11; -1. ° Lời giải ví dụ 2 (bài 102 trang 97 SGK Toán 6 Tập 1): – Nhận thấy nếu số nguyên b là ước của số nguyên a thì –b cũng là ước của số nguyên a. – Đồng thời b là ước của a thì b cũng là ước của |a| và ngược lại. ⇒ Như vậy, để tìm các ước của một số nguyên a, ta chỉ cần tìm các ước dương của |a| rồi thêm các số đối của chúng thì ta được các ước của số nguyên a. – Các ước dương của 3 là: 1; 3. ⇒ Ư(–3) = {1; 3; –1; –3} – Các ước dương của 6 là: 1 ; 2 ; 3 ; 6. ⇒ Ư(6) = {1 ; 2 ; 3 ; 6 ; –1; –2; –3; –6} – Các ước dương của 11 là : 1 ; 11 ⇒ Ư(11) = {1 ; 11 ; –1; –11} – Các ước dương của 1 là 1. ⇒ Ư(–1) = {1; –1} Hy vọng một số dạng bài tập số nguyên, phép toán cộng trừ số nguyên âm cơ bản và nâng cao ở trên hữu ích cho các em trong việc học tập. Mọi góp ý và có câu hỏi nào các em hãy để lại bình luận dưới bài viết để được ghi nhận và hỗ trợ, chúc các em học tốt. Đăng bởi: Mầm Non Ánh Dương Chuyên mục: Giáo Dục
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục