Trong hình học, đường tròn chính là tập hợp tất cả các điểm cùng nằm trên một mặt phẳng, cách đều một điểm cho trước bằng một khoảng cách bất kỳ. Vậy đường tròn có bao nhiêu trục đối xứng? Chúng ta hãy cùng tìm hiểu câu trả lời qua bài viết dưới đây nhé!
Định nghĩa đường tròn
Đường tròn là một hình elip đặc biệt có 2 tiêu điểm trùng nhau và tâm sai của nó bằng 0. Hoặc đường tròn cũng chính là hình bao quanh nhiều diện tích nhất trên mỗi đơn vị chu vi bình phương
This post: Đường tròn có bao nhiêu trục đối xứng? Trục đối xứng của đường tròn là gì?
Xác định đường tròn: Một đường tròn được xác định khi biết tâm và bán kính của nó, hoặc khi biết một đoạn thẳng chính là đường kính của đường tròn.
Đường tròn tâm O bán kính R, kí hiệu (O;R), là hình gồm các điểm cách O một khoảng bằng R.
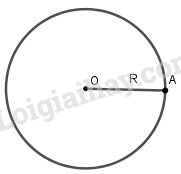
- Nếu A nằm trên đường tròn (O;R) thì OA=R
- Nếu A nằm trong đường tròn (O; R) thì OA<R
- Nếu A nằm ngoài đường tròn (O;R) thì OA>R.
Đường tròn có bao nhiêu trục đối xứng?
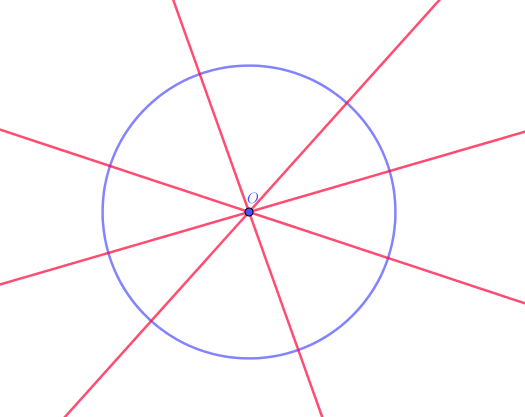
Lời giải đáp cho câu hỏi đường tròn có bao nhiêu trục đối xứng chính là: Trục đối xứng đường tròn là đường kính của đường tròn. Mà một đường tròn có vô số đường kính nên có vô số trục đối xứng.
Ví Dụ: Cho một đường thẳng d là đường trung trực của đoạn thẳng MN thì điểm M đối xứng với điểm N qua đường thẳng d. Khi đó đường thẳng d được gọi là trục đối xứng của hai điểm M và N. Hoặc hai điểm được gọi là đối xứng với nhau qua một đường thẳng nếu đường thẳng đó là đường trung trực của đoạn thẳng nối với hai điểm đó. Đối xứng này chính là đối xứng trục.
Định lí về sự xác định một đường tròn
Qua ba điểm không thẳng hàng, ta vẽ được một và chỉ một đường tròn.
Tâm O của đường tròn đi qua ba điểm A, B, C là giao điểm của ba đường trung trực của tam giác ABC.
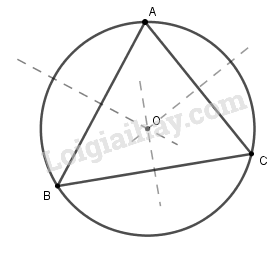
Tính chất đối xứng của đường tròn
a) Tâm đối xứng
Đường tròn là hình có tâm đối xứng. Tâm của đường tròn là tâm đối xứng của đường tròn đó.
b) Trục đối xứng
Đường tròn là hình có trục đối xứng. Bất kì đường kính nào cũng là trục đối xứng của đường tròn.
Chú ý:
* Trong tam giác vuông trung điểm cạnh huyền là tâm đường tròn ngoại tiếp.
* Trong tam giác đều , tâm đường tròn ngoại tiếp là trọng tâm tam giác đó.
Đối xứng trục
Khi đường thẳng d là đường trung trực của đoạn thẳng AB thì điểm A đối xứng với điểm B qua đường thẳng d. Khi đó đường thẳng d gọi là trục đối xứng của hai điểm A và B.
Nói cách khác, hai điểm được gọi là đối xứng với nhau qua một đường thẳng nếu đường thẳng đó là đường trung trực của đoạn thẳng nối hai điểm đó. Đối xứng này gọi là đối xứng trục.
Hai hình đối xứng qua một đường thẳng
Hai hình gọi là đối xứng với nhau qua một đường thẳng nếu mỗi điểm của hình này đối xứng với một điểm thuộc hình kia, và ngược lại. Đây cũng gọi là đối xứng trục.
Hình có trục đối xứng
Định nghĩa
Hai điểm được gọi là đối xứng với nhau qua đường thẳng d nếu d là đường trụng trực của đoạn thẳng nối hai điểm đó.
Trục đối xứng của một số hình
- Đường tròn, trục đối xứng là đường kính của đường tròn. Đường tròn có vô số trục đối xứng.
- Tam giác cân, trục đối xứng là đường cao, trung trực, trung tuyến, phân giác của tam giác cân xuất phát từ đỉnh ứng với cạnh đáy. Tam giác cân có duy nhất 1 trục đối xứng.
- Tam giác đều, trục đối xứng là đường cao, trung trực, trung tuyến, phân giác của tam giác đều. Tam giác đều có 3 trục đối xứng.
- Hình thang cân, trục đối xứng là đường thẳng đi qua trung điểm hai đáy của hình thang cân. Hình thang cân có 1 trục đối xứng.
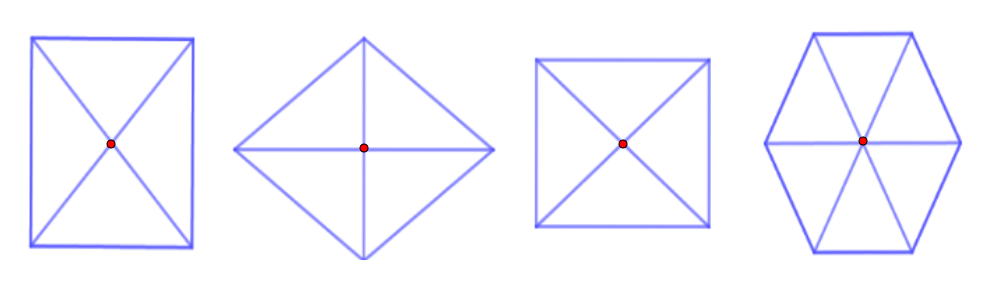
- Hình thoi, trục đối xứng là hai đường chéo của hình thoi. Hình thoi có 2 trục đối xứng.
- Hình vuông, trục đối xứng là hai đường chéo của hình vuông và hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình vuông. Hình vuông có 4 trục đối xứng.
- Hình chữ nhật, trục đối xứng là hai đường thẳng đi qua trung điểm từng cặp cạnh đối diện của hình chữ nhật. Hình chữ nhật có 2 trục đối xứng.
- Đa giác đều n cạnh thì có n trục đối xứng
Một số định lý liên quan đến đối xứng trục (hình học)
Định lý Colling
Các đường thẳng là đối xứng của một đường thẳng qua ba cạnh của tam giác đồng quy khi và chỉ khi đường thẳng này đi qua trực tâm của tam giác. Trong trường hợp này điểm đồng quy nằm trên đường tròn ngoại tiếp tam giác.
Định lý Bliss
Cho ba đường thẳng song song đi qua ba trung điểm của ba cạnh của tam giác khi đó các đường thẳng đối xứng của ba cạnh tam giác đó qua ba đường thẳng này một cách lần lượt sẽ đồng quy tại đường tròn chín điểm của tam giác đó.
Định lý Paul Yiu
Cho đường thẳng qua tâm nội tiếp của tam giác và cắt ba cạnh BC, CA, AB của tam giác lần lượt tại X, Y, Z. Lấy các điểm X’, Y’, Z’ là đối xứng của X, Y, Z qua ba đường phân giác tương ứng. Khi đó ba điểm X’, Y’, y’ thẳng hàng.
Lịch sử về đường tròn
Từ circle có nguồn gốc từ tiếng Hy Lap κίρκος/κύκλος (kirkos/kuklos), nghĩa là “vòng” hay “nhẫn”.
Đường tròn đã được biết đến từ trước khi lịch sử ghi nhận được. Những hình tròn trong tự nhiên hẳn đã được quan sát, ví dụ như Mặt Trăng, Mặt Trời… Đường tròn là nền tảng để phát triển bánh xe, mà cùng với những phát minh tương tự như bánh răng, là thành phần quan trọng trong máy móc hiện đại. Trong toán học, việc nghiên cứu đường tròn đã dẫn đến sự phát triển của hình học, thiên văn học và vi tích phân.
Khoa học sơ khai, đặc biệt là hình học, thiên văn học và chiêm tinh học, thường được nhiều học giả thời trung cổ kết nối với thánh thần, và nhiều người tin rằng có gì đó “thiêng liêng” và “hoàn hảo” ở hình tròn.
Một số dấu mốc trong lịch sử đường tròn:
- Năm 1700 trước Công nguyên– Bản giấy cói Rhind đưa ra phương pháp để tính diện tích hình tròn. Kết quả tương đương với 256/81 (3.16049…) như một giá trị xấp xỉ của π.
- Năm 300 trước Công nguyên – Quyển 1, Quyển 3 của bộ sách Cơ sở của Euclid đưa ra định nghĩa và bàn về những tính chất của đường tròn.
- Trong Bức thư thứ bảy của Plato có một định nghĩa chi tiết và giải thích về đường tròn. Plato viết về một đường tròn hoàn hảo, và sự khác biệt của nó với bất kì hình vẽ, giải thích hay định nghĩa nào khác.
- Năm 1880 – Lindemann chứng minh được π là số siêu việt, giải quyết trọn vẹn bài toán cầu phương hình tròn sau hơn một thiên niên kỷ.
Tìm hiểu về hình học

Hình học là một phân nhánh của toán học liên quan đến các câu hỏi về hình dạng, kích thước, vị trí tương đối của các hình khối, và các tính chất của không gian. Hình học phát triển độc lập trong một số nền văn hóa cổ đại như một phần của kiến thức thực tiễn liên quan đến chiều dài, diện tích, và thể tích, với một phần các yếu tố của khoa học Toán học đến từ phương Tây như các định lý của Thales (thế kỷ VI TCN). Đến thế kỷ thứ III TCN, hình học đã được Euclid hệ thống hóa dưới một hình thức tiên đề mang tên ông – Hình học Euclid đã trở thành chuẩn mực cho nhiều thế kỷ sau đó. Archimedes phát triển các kỹ thuật rất khéo léo để tính diện tích và khối lượng, theo một cách nào đó đã áp dụng phép tính tích phân.
Thiên văn học khi tính toán vị trí của các ngôi sao và hành tinh trên bản đồ thiên cầu và mô tả mối quan hệ giữa chuyển động của các thiên thể, đã trở thành một nguồn quan trọng cung cấp các bài toán hình học trong suốt 1500 năm tiếp theo. Trong thế giới cổ điển, cả hình học và thiên văn học đã được coi là một phần của quadrivium, một tập hợp con của bảy môn giáo dục khai phóng cần thiết cho mọi công dân phải nắm vững.
Việc giới thiệu hệ tọa độ của René Descartes và sự phát triển đồng thời của đại số đánh dấu một giai đoạn phát triển mới cho hình học, kể từ khi các hình hình học như các đường cong phẳng không thể được mô tả bằng giải tích theo dạng phương trình và hàm. Điều này đóng một vai trò quan trọng trong sự xuất hiện của vi tích phân vào thế kỷ XVII. Sau đó, lý thuyết của phối cảnh cho thấy rằng có nhiều yếu tố hình học hơn là chỉ các thuộc tính số liệu của các hình vẽ: phối cảnh đã trở thành nguồn gốc của hình học projective. Các đối tượng nghiên cứu của hình học đã được tiếp tục mở rộng bằng việc nghiên cứu các cấu trúc nội tại của các đối tượng hình học của Euler và Gauss, điều này dẫn đến việc tạo ra các nhánh tô pô học và hình học vi phân.
Trong thời của Euclid, không sự phân biệt rõ ràng giữa không gian vật lý và không gian hình học. Kể từ khi phát hiện hình học phi Euclid vào thế kỷ 19, các khái niệm về không gian đã trải qua một sự thay đổi cơ bản và nêu lên câu hỏi: không gian hình học nào là thích hợp nhất với không gian vật lý. Với sự phát triển của toán học lý thuyết trong thế kỷ 20, ‘không gian’ (cho dù là ‘điểm’, ‘đường’, hoặc ‘mặt phẳng’) bị mất nội dung trực quan của nó, vì vậy người đọc phải phân biệt giữa không gian vật lý và không gian hình học (trong đó ‘không gian’, ‘điểm’, v.v… vẫn còn có ý nghĩa trực quan) và không gian trừu tượng. Hình học hiện đại xem xét không gian đa tạp – không gian có mức độ trừu tượng đáng kể hơn so với không gian Euclid quen thuộc. Những không gian trên có thể có sẵn các cấu trúc bổ sung nhằm cho phép đo chiều dài. Hình học hiện đại có nhiều mối quan hệ với vật lý như được minh họa bằng các liên kết giữa hình học giả Riemann và thuyết tương đối rộng. Một trong những lý thuyết vật lý mới nhất, lý thuyết dây, cũng rất gần gũi với hình học.
Trong khi bản chất thị giác của hình học làm cho nó dễ dàng tiếp cận hơn so với các môn toán học khác như đại số hay lý thuyết số, ngôn ngữ hình học cũng được sử dụng trong bối cảnh xa rời truyền thống nguồn gốc Euclide của nó (ví dụ như trong hình học fractal và hình học đại số).
Khởi đầu sớm nhất được ghi nhận của bộ môn hình học có thể được truy nguồn từ các nền văn minh cổ đại Lưỡng Hà và Ai Cập vào thiên niên kỷ thứ 2 TCN. Hình học sơ khai là một tập hợp các nguyên tắc thực nghiệm được phát minh liên quan đến độ dài, góc, diện tích, và khối lượng. Chúng được phát triển để đáp ứng một số nhu cầu thực tế trong khảo sát, xây dựng, thiên văn học và hàng loạt ngành nghề khác. Các sách vở sớm nhất được biết đến về hình học là giấy cói Rhind (2000–1800 TCN) ở Ai Cập và giấy cói Moscow (khoảng 1890 TCN), các sách đất sét Babylon như “Plimpton 322” (1900 TCN). Ví dụ, giấy cói Moscow đưa ra một công thức tính thể tích của một hình chóp cụt. Các tấm đất sét sau đó (350–50 TCN) cho thấy các nhà thiên văn Babylon đã sử dụng hình thang để tính toán vị trí và li độ của sao Mộc trong không gian thời gian-vận tốc. Các phép tính hình học này đã đi trước các tính toán của Máy tính Oxford, bao gồm định lý tốc độ trung bình, những 14 thế kỷ. Người Nubia cổ đại ở Nam Ai Cập đã thành lập một hệ thống hình học bao gồm cả phiên bản sơ khai của đồng hồ mặt trời.
Video về đường tròn có bao nhiêu trục đối xứng?
Kết luận
Những thông tin trên hy vọng đã giúp cho các bạn biết được đường tròn có bao nhiêu trục đối xứng. Nếu thấy thông tin hữu ích, hãy chia sẻ ngay với bạn bè nhé. Xin cảm ơn!
Bản quyền bài viết thuộc trường THPT thành Phố Sóc Trăng. Mọi hành vi sao chép đều là gian lận!
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục




