Phương trình trùng phương là gì? Cách giải phương trình trùng phương cực hay
Bài viết trước Mầm Non Ánh Dương đã giới thiệu đến quý thầy cô và các bạn học sinh cách giải phương trình bậc bốn nhanh nhất. Tiếp tục mạch kiến thức đó, bài viết hôm nay, chúng tôi sẽ giới thiệu về phương trình trùng phương và cách giải phương trình trùng phương cực hay. Bạn theo dõi nhé !
I. PHƯƠNG TRÌNH TRÙNG PHƯƠNG LÀ GÌ?
This post: Phương trình trùng phương là gì? Cách giải phương trình trùng phương cực hay
Phương trình trùng phương là phương trình có dạng: 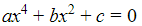
Đặt t = x2 (t >0) Ta được phương trình: 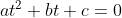 (2)
(2)
Phương trình (1) có 4 nghiệm phân biệt, phương trình (2) có hai nghiệm dương phân biệt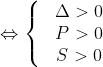
Phương trình (1) có 3 nghiệm phân biệt 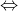 (2) có một nghiệm dương và một nghiệm bằng 0
(2) có một nghiệm dương và một nghiệm bằng 0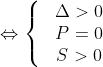
Phương trình (1) có 2 nghiệm phân biệt 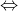 (2) có một một nghiệm kép dương hoặc có ai nghiệm trái dấu
(2) có một một nghiệm kép dương hoặc có ai nghiệm trái dấu![ec42b0e5af94d17fcd610289e976b488-2-2 Leftrightarrow left[ begin{matrix} & left{ begin{matrix} & Delta =0 & S>0 end{align} right. & P<0 end{align} right.]](https://mamnonanhduongvt.edu.vn/wp-content/uploads/2022/08/ec42b0e5af94d17fcd610289e976b488-2-2.gif)
Phương trình (1) có 1 nghiệm 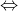 (2) có một nghiệm kép bằng 0 hoặc có một nghiệm bằng không và nghiệm còn lại âm
(2) có một nghiệm kép bằng 0 hoặc có một nghiệm bằng không và nghiệm còn lại âm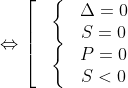
Phương trình (1) có 1 nghiệm 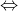 (2) vô nghiệm hoặc có hai nghiệm âm
(2) vô nghiệm hoặc có hai nghiệm âm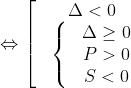
II. CÁCH GIẢI PHƯƠNG TRÌNH TRÙNG PHƯƠNG CỰC HAY

Phương pháp 1: Đưa phương trình trùng phương về dạng phương trình tích
- Dựa vào phương trình ban đầu, ta sẽ biến đổi bằng cách đặt nhân tử chung, sử dụng hằng đẳng thức,… để được phương trình mới có dạng một tích của các biểu thức. Sau đó tiến hành giải phương trình mới.
- Tổng quát: A.B = 0 ⇔ A = 0 hoặc B=0
Phương pháp 2: Giải phương trình trùng phương bằng phương pháp đặt ẩn
Ta có: 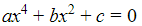 với a ≠ 0
với a ≠ 0
- Bước 1: Đặt ẩn t = x² với điều kiện t ≥ 0
- Bước 2: Tiến hành giải phương trình bậc 2 ẩn t: at² + bt + c = 0 để tìm t
- Bước 3: Tìm ra giá trị x thỏa mãn điều kiện t = x² (t ≥ 0)bằng cách giải phương trình t = x²
- Bước 4: Kết luận nghiệm của phương trình trùng phương
***Lưu ý: Đối với tất cả các dạng bài toán về phương trình trùng phương giải theo cách đặt ẩn, học sinh cần thực hiện theo đủ 4 bước như trên để đạt điểm trình bày tối đa.
III. BÀI TẬP VẬN DỤNG
Bài 1: Cho phương trình: 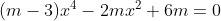 . Tìm m để phương trình có nghiệm
. Tìm m để phương trình có nghiệm
Hướng dẫn:
Trường hợp1: Xét m – 3 = 0
Trường hợp 2: Xét 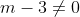
Đặt 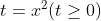 Ta có phương trình
Ta có phương trình 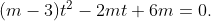
Để phương trình có nghiệm thì phương trình (2) phải có ít nhất một nghiệm không âm
Khi đó ta cần * PT (2) có hai nghiệm trái dấu KQ: 0 < m < 3
Hoặc PT (2) có nghiệm bằng 0 KQ:m = 0
Hoặc PT (2) có hai nghiệm dương KQ: 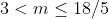
Bài 2. Cho phương trình 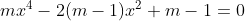 .Tìm m để phương trình
.Tìm m để phương trình
a) có nghiệm duy nhất b) có hai nghiệm phân biệt c) có 3 nghiệm phân biệt d) có 4 nghiệm phận biệt
Hướng dẫn:
Trường hợp1:: m = 0 PT có 2 nghiệm pb
Trường hợp 2: 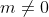
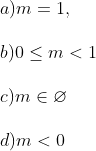
Bài 3: Giải phương trình 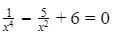
Điều kiện: x ≠ 0
Ta có 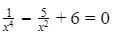 ⇔
⇔ 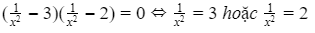
⇔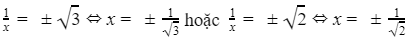
Vậy phương trình có 4 nghiệm phân biệt lần lượt là 
Bài 4: Giải phương trình 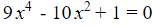
- Bước 1: Đặt t = (x)² điều kiện t ≥ 0
- Bước 2: Ta có phương trình mới: 9t² – 10t + 1 = 0 (1)
- Giải phương trình (1), ta có: (t – 1)(9t – 1) = 0
- Với t =1 thỏa mãn điều kiện t ≥ 0
- Với t = 1/9 thỏa mãn điều kiện t ≥ 0
- Bước 3: Tìm x
- Vì t = 1 nên x² = 1 ⇔ x = ±1
- Vì t = 1/9 nên x² = 1/9 ⇔ x = ±1⁄3
- Bước 4: Vậy phương trình 9×4 – 10×2+ 1 = 0 có 4 nghiệm phân biệt S={-1; -1/3; 1/3; 1}
Bài 5: Giải phương trình 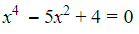
Lời giải:
- Bước 1: Đặt t = x² điều kiện t ≥ 0
- Bước 2: Ta có phương trình mới: t² – 5t + 4 = 0 (1)
- Giải phương trình (1): (t – 1)(t – 4) = 0 ⇔ t = 1 hoặc t = 4
- Với t = 1 hoặc t = 4 thỏa mãn điều kiện t0
- Bước 3: Tìm x
- Với t = 1 ⇔ x² = 1 ⇔ x = ±1
- Với t = 4 ⇔ x² = 4 ⇔ x = ±2
- Bước 4: Vậy phương trình
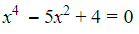 có 4 nghiệm phân biệt S = {-2; -1; 1; 2}
có 4 nghiệm phân biệt S = {-2; -1; 1; 2}
Bài 6: Giải phương trình 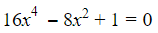
Lời giải:
Ta có: 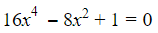 ⇔
⇔ 
- Bước 1: Đặt t = (2x)² điều kiện t ≥ 0
- Bước 2: Ta có phương trình mới: t² – 2t + 1 = 0 (1)
- Giải phương trình (1) (t – 1)² = 0 ⇔ t = 1
- Với t = 1 thỏa mãn điều kiện t ≥ 0
- Bước 3: Tìm x
- Với t = 1 ⇔ (2x)²=1 ⇔ x = ±1 ⇔ x = 0.5 hoặc x = – 0.5
- Bước 4: Vậy phương trình
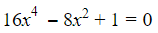 có 2 nghiệm phân biệt S = {-0.5; 0.5}
có 2 nghiệm phân biệt S = {-0.5; 0.5}
Bài 7: Giải phương trình trùng phương:
Lời giải:
Đặt
Phương trình trở thành (1)
Có
Phương trình (1) có hai nghiệm phân biệt:
(tm) và
(loại)
Với
Vậy phương trình có hai nghiệm phân biệt x = 1 hoặc x = -1
Bài 8: Giải và biện luận theo m số nghiệm của phương trình:
Lời giải:
Với , phương trình đã cho trở thành:
(loại)
Với , phương trình đã cho là phương trình trùng phương:
(1)
Đặt
Phương trình trở thành (2)
Có ,
và
Có P khác 0 nên phương trình không có nghiệm bằng 0 nên phương trình (1) không có 3 nghiệm phân biệt hoặc 1 nghiệm
Phương trình (1) có 4 nghiệm phân biệt khi và chỉ khi phương trình (2) có hai nghiệm phân biệt dương
Phương trình (1) vô nghiệm khi và chỉ khi phương trình (2) vô nghiệm hoặc hai nghiệm phân biệt âm
Vậy với thì phương trình (1) có hai nghiệm phân biệt
, phương trình (1) có bốn nghiệm phân biệt
, phương trình (1) vô nghiệm
Vậy là các quý thầy cô cùng các bạn học sinh đã được chia sẻ lý thuyết về phương trình trùng phương và cách giải phương trình trùng phương cực hay. Hi vọng, đây là nguồn tư liệu quý phục vụ cho quý trình dạy và học. Xem thêm cách giải phương trình bậc bốn nữa nhé !
Bản quyền bài viết thuộc trường Mầm Non Ánh Dương. Mọi hành vi sao chép đều là gian lận.
Nguồn chia sẻ: Trường Mầm Non Ánh Dương (mamnonanhduongvt.edu.vn)
Source: Mamnonanhduongvt.edu.vn
Category: Giáo dục